
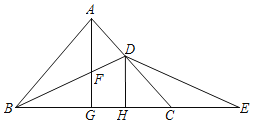
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,点E是BC延长线上的一点,且BD=DE.点G是线段BC的中点,连结AG,交BD于点F,过点D作DH⊥BC,垂足为H.
(1)求证:△DCE为等腰三角形;
(2)若∠CDE=22.5°,DC=![]() ,求GH的长;
,求GH的长;
(3)探究线段CE,GH的数量关系并用等式表示,并说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)CE=2GH,理由见解析.
;(3)CE=2GH,理由见解析.
【解析】
(1)根据题意可得∠CBD=![]() ∠ABC=
∠ABC=![]() ∠ACB,,由BD=DE,可得∠DBC=∠E=
∠ACB,,由BD=DE,可得∠DBC=∠E=![]() ∠ACB,根据三角形的外角性质可得∠CDE=
∠ACB,根据三角形的外角性质可得∠CDE=![]() ∠ACB=∠E,可证△DCE为等腰三角形;
∠ACB=∠E,可证△DCE为等腰三角形;
(2)根据题意可得CH=DH=1,△ABC是等腰直角三角形,由等腰三角形的性质可得BG=GC,BH=HE=![]() +1,即可求GH的值;
+1,即可求GH的值;
(3)CE=2GH,根据等腰三角形的性可得BG=GC,BH=HE,可得GH=GC﹣HC=GC﹣(HE﹣CE)=![]() BC﹣
BC﹣![]() BE+CE=
BE+CE=![]() CE,即CE=2GH
CE,即CE=2GH
证明:(1)∵AB=AC,
∴∠ABC=∠ACB,
∵BD平分∠ABC,
∴∠CBD=![]() ∠ABC=
∠ABC=![]() ∠ACB,
∠ACB,
∵BD=DE,
∴∠DBC=∠E=![]() ∠ACB,
∠ACB,
∵∠ACB=∠E+∠CDE,
∴∠CDE=![]() ∠ACB=∠E,
∠ACB=∠E,
∴CD=CE,
∴△DCE是等腰三角形
(2)
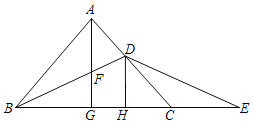
∵∠CDE=22.5°,CD=CE=![]() ,
,
∴∠DCH=45°,且DH⊥BC,
∴∠HDC=∠DCH=45°
∴DH=CH,
∵DH2+CH2=DC2=2,
∴DH=CH=1,
∵∠ABC=∠DCH=45°
∴△ABC是等腰直角三角形,
又∵点G是BC 中点
∴AG⊥BC,AG=GC=BG,
∵BD=DE,DH⊥BC
∴BH=HE=![]() +1
+1
∵BH=BG+GH=CG+GH=CH+GH+GH=![]() +1
+1
∴1+2GH=![]() +1
+1
∴GH=![]()
(3)CE=2GH
理由如下:∵AB=CA,点G 是BC的中点,
∴BG=GC,
∵BD=DE,DH⊥BC,
∴BH=HE,
∵GH=GC﹣HC=GC﹣(HE﹣CE)=![]() BC﹣
BC﹣![]() BE+CE=
BE+CE=![]() CE,
CE,
∴CE=2GH


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三个角是∠A,∠B,∠C ,它们所对的边分别是a,b,c.①c2-a2=b2;②∠A=![]() ∠B=
∠B=![]() ∠C;③c=
∠C;③c=![]() a=
a=![]() b;④a=2,b=2
b;④a=2,b=2 ![]() ,c=
,c=![]() .上述四个条件中,能判定△ABC 为直角三角形的有( )
.上述四个条件中,能判定△ABC 为直角三角形的有( )
A. 1个 B. 2个
C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
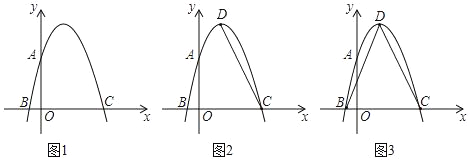
【题目】如图1,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+bx+3交x轴于B、C两点(点B在左,点C在右),交y轴于点A,且OA=OC,B(﹣1,0).
(1)求此抛物线的解析式;
(2)如图2,点D为抛物线的顶点,连接CD,点P是抛物线上一动点,且在C、D两点之间运动,过点P作PE∥y轴交线段CD于点E,设点P的横坐标为t,线段PE长为d,写出d与t的关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,连接BD,在BD上有一动点Q,且DQ=CE,连接EQ,当∠BQE+∠DEQ=90°时,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m+3)x+3m=0.
(1)求证:无论m取什么实数值,该方程总有两个实数根.
(2)若该方程的两实根x1和x2是一个矩形两邻边的长且该矩形的对角线长为![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在 ![]() 中,
中, ![]() ,AC=BC,
,AC=BC, ![]() ,
, ![]() ,垂足分别为D,E.
,垂足分别为D,E.
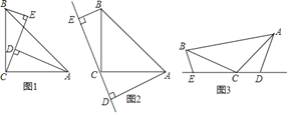
(1)若AD=2.5cm,DE=1.7cm,求BE的长.
(2)如图2,在原题其他条件不变的前提下,将CE所在直线旋转到 ![]() ABC的外部,请你猜想AD,DE,BE三者之间的数量关系,直接写出结论:________.(不需证明)
ABC的外部,请你猜想AD,DE,BE三者之间的数量关系,直接写出结论:________.(不需证明)
(3)如图3,若将原题中的条件改为:“在 ![]() ABC中,AC=BC,D,C,E三点在同一条直线上,并且有
ABC中,AC=BC,D,C,E三点在同一条直线上,并且有 ![]() ,其中
,其中 ![]() 为任意钝角”,那么(2)中你的猜想是否还成立?若成立,请予以证明;若不成立,请说明理由.
为任意钝角”,那么(2)中你的猜想是否还成立?若成立,请予以证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究下面的问题:
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(a>b),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是________(用式子表示),即乘法公式中的___________公式.
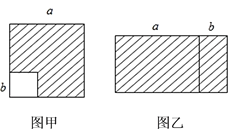
(2)运用你所得到的公式计算:
①10.7×9.3
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
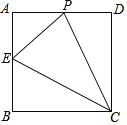
【题目】如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿![]() 移动至终点C.设点P经过的路径长为x,
移动至终点C.设点P经过的路径长为x,![]() 的面积为y,则下列图象能大致反映y与x之间的函数关系的是( )
的面积为y,则下列图象能大致反映y与x之间的函数关系的是( )
A.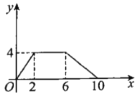 B.
B.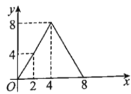
C.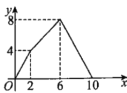 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com