
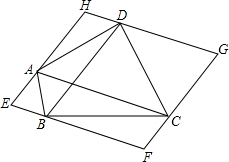
 ��ͼ�����ı���ABCD���ĸ�����ֱ����Խ���AC��BD��ƽ���ߣ��õ��ı���EFGH��
��ͼ�����ı���ABCD���ĸ�����ֱ����Խ���AC��BD��ƽ���ߣ��õ��ı���EFGH������ ��1������֤���ı���EFGH��ƽ���ı��Σ�Ȼ����ݵ������εĶԽ�����ȣ�����֤��ƽ���ı���EFGH���ڱ���ȣ�����֤�ã�
��2������ƽ���ı����Լ������ε������ʽ����֤�ã�
��3�����ݣ�2���Ĺ��̼�����⣮
��� �⣺��1���ı���EFGH����״Ϊ���Σ�
�����ǣ���HG��AC��EF��EH��BD��GF��
���ı���EFGH��ƽ���ı��Σ��ı���AHGC��ƽ���ı��Σ�
��AC=GH��
ͬ����EH=BD��
�֡ߵ�������ABCD�У�AC=BD��
��EH=HG��
��ƽ���ı���EFGH�����Σ�
��2�����ı���AHGC��ƽ���ı��Σ�
��S��ACD=$\frac{1}{2}$Sƽ���ı���AHGC��
ͬ����S��ABC=$\frac{1}{2}$Sƽ���ı���AEFC��
��S�ı���EFGH=2S�ı���ABCD=12��
ͬ�������ı���EFGH�����Ϊ6�����ı���ABCD�����Ϊ3��
�ʴ��ǣ�12��3��
��3��S�ı���EFGH=2S�ı���ABCD��
���� ���⿼�������ε��ж���������ε����ʣ�����ƽ���ı��κ������ε������ʽ֤��S�ı���EFGH=2S�ı���ABCD�ǹؼ���


 ������ϵ�д�
������ϵ�д� �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �Ķ�����IJ��ϣ�
�Ķ�����IJ��ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=$\frac{2}{x}$ | B�� | y=x+2 | C�� | y=x2 | D�� | y=2x |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com