
【题目】如图1,直线AB与x轴、y轴分别交于点A(3,0)、B,动点P从原点出发,以每秒1个单位长度的速度向点A运动,到达点A立即停止.点C(﹣1,0),以P为直角顶点,PC为直角边向x轴上方作等腰Rt△PQC,△PQC与△AOB重叠部分面积为S,点P运动时间为t(秒),S关于t的函数图象如图2所示(其中0≤t≤![]() ,
,![]() ≤t≤3时,函数解析式不同).
≤t≤3时,函数解析式不同).
(1)当t=![]() 时,S的值为 ;
时,S的值为 ;
(2)求直线AB的解析式;
(3)求S关于t的解析式,并写出t的取值范围.

【答案】(1)![]() ;(2)y=﹣
;(2)y=﹣![]() x+4;(3)
x+4;(3)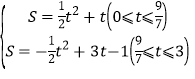 .
.
【解析】
(1)由图2可知:当t=![]() 时,Q在AB上,画图1,根据面积差可得结论;
时,Q在AB上,画图1,根据面积差可得结论;
(2)先根据平行相似计算OB的长,得点B的坐标,利用待定系数法可得结论;
(3)分两种情况:0≤t≤![]() ,
,![]() ≤t≤3时,分别根据面积差可得对应解析式.
≤t≤3时,分别根据面积差可得对应解析式.
解:(1)当Q在AB上时,如图1,
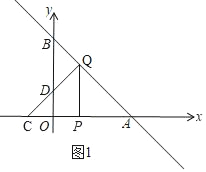
由题意得:OP=![]() ,OC=1,
,OC=1,
∴PC=PQ=1+![]() =
=![]() ,
,
∵△PQC和△COD都是等腰直角三角形,
∴S=S△PCQ﹣S△COD=![]()
![]()
![]()
![]()
![]() ﹣
﹣![]()
![]() 1
1![]() 1=
1=![]() ,
,
故答案为:![]() ;
;
(2)∵A(3,0),
∴OA=3,
∴AP=3﹣![]() =
=![]() ,
,
∵PQ∥OB,
∴△AQP∽△ABO,
∴![]() ,
,
∴![]() ,OB=4,
,OB=4,
∴B(0,4),
设直线AB的解析式为:y=kx+b,
把A(3,0)、B(0,4)代入得:![]() ,
,
解得: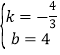 ,
,
∴直线AB的解析式为:y=﹣![]() x+4;
x+4;
(3)由题意得:OP=t,
当0≤t≤![]() 时,如图2,
时,如图2,
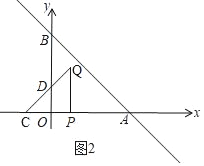
△PQC与△AOB重叠部分是梯形ODQP,
S=S△PCQ﹣S△COD=![]() (t+1)2-
(t+1)2-![]() ×1×1=
×1×1=![]() t2+t;
t2+t;
当![]() ≤t≤3时,如图3,
≤t≤3时,如图3,
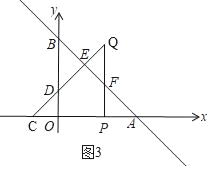
△PQC与△AOB重叠部分是五边形ODEFP,
∵OP=t,AP=PF=3﹣t,
∴FQ=t+1﹣(3﹣t)=2t﹣2,
∵∠Q=∠EFQ=∠AFP=45°,
∴∠FEQ=90°,
∴EQ=EF=![]() ,
,
S=S△PCQ﹣S△COD﹣S△EFQ=![]() t2+t﹣
t2+t﹣![]() =﹣
=﹣![]() +3t﹣1;
+3t﹣1;
综上,S关于t的解析式为: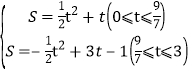 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
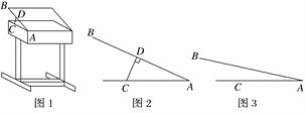
【题目】某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30 cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长;
(2)如图3,当∠BAC=12°时,求AD的长.(结果保留根号)
(参考数据:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
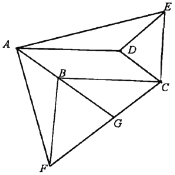
【题目】如图,在口ABCD中,分别以边BC,CD作等腰△BCF,△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,连接AF,AE.
(1)求证:△ABF≌△EDA;
(2)延长AB与CF相交于G,若AF⊥AE,求证BF⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
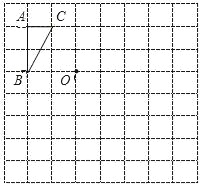
【题目】如图8×8正方形网格中,点A、B、C和O都为格点.
(1)利用位似作图的方法,以点O为位似中心,可将格点三角形ABC扩大为原来的2倍.请你在网格中完成以上的作图(点A、B、C的对应点分别用A′、B′、C′表示);
(2)当以点O为原点建立平面坐标系后,点C的坐标为(﹣1,2),则A′、B′、C′三点的坐标分别为:A′: B′: C′: .
查看答案和解析>>
科目:初中数学 来源: 题型:
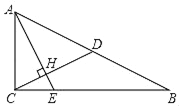
【题目】如图,在Rt△ABC中,∠ACB=9O°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB交于H、E两点,且AH=2CH,若AB=2![]() ,则BE的值为_____.
,则BE的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电视节目“奔跑吧兄弟”播出后深受中小学生的喜爱,小刚想知道大家最喜欢哪位“兄弟”,于是在本校随机抽取了一部分学生进行抽查(每人只能选一个自己最喜欢的“兄弟”),将调查结果进行了整理后绘制成如图两幅不完整的统计图,请结合图中提供的信息解答下列问题:
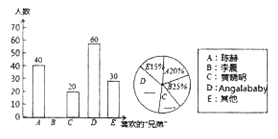
(1)本次被调查的学生有_______人.
(2)将两幅统计图补充完整.
(3)若从3名喜欢“李晨”的学生和2名喜欢“![]() ”的学生中随机抽取两人参加文体活动,用树状图或列表法求出两人都是喜欢“李晨”的学生的概率.
”的学生中随机抽取两人参加文体活动,用树状图或列表法求出两人都是喜欢“李晨”的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广安市红色旅游资源丰富,无论是小平故里行,还是华蓥山上游,都吸引了不少游客。2014~2018年旅游收入不断增长,同比增速分别为:17.3%,14.7%,17.3%,16.5%,19.1%,关于这组数据,下列说法正确的是( ).
A. 中位数是14.7%B. 众数是17.3%
C. 平均数是17.98%D. 方差是0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com