
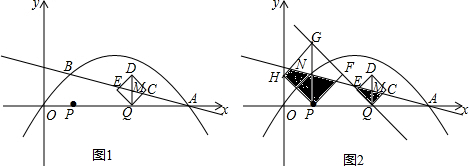
分析 (1)待定系数法直接求出;
(2)设AB与y轴交于点X,则△XOA∽△MQA,利用相似比例求MQ的长度即可求出正方形QCDE的面积;
(3)①由于阴影部分是两个相似的梯形,且相似比可求,所以只要求出其中一个梯形的面积即可.
②将边的重合转化为点的相遇:延长DE交x轴于点R,P与R相遇即DE与PF重合,紧接着P与Q相遇时,PH与FQ,FP与CQ重合,路程可求,速度之比已知,则P点在这两次的运动路程也就可求,从而坐标也就确定了.
解答 解:(1)
设抛物线的解析式为y=ax2+bx,
将点A(10,0)和点B(2,2)代入y=ax2+bx可得:$\left\{\begin{array}{l}{100a+10b=0}\\{4a+2b=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-\frac{1}{8}}\\{b=\frac{5}{4}}\end{array}\right.$,
∴抛物线的解析式为$y=-\frac{1}{8}{x}^{2}+\frac{5}{4}x$;
(2)设直线AB的解析式为y=kx+h,
将点A(10,0)和点B(2,2)代入y=kx+h可得:$\left\{\begin{array}{l}{10k+h=0}\\{2k+h=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{1}{4}}\\{h=\frac{5}{2}}\end{array}\right.$,
∴直线AB的解析式为:$y=-\frac{1}{4}x+\frac{5}{2}$;
设直线AB与y轴交于点X,如图1,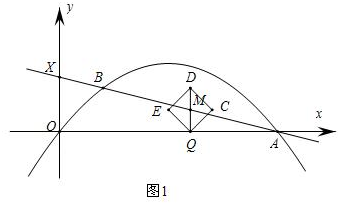
则X(0,$\frac{5}{2}$),
∵P(m,0),
∴OP=m,
∵AQ=2OP,
∴AQ=2m,
∵△XOA∽△MQA,
∴$\frac{MQ}{AQ}=\frac{XO}{AO}=\frac{1}{4}$,
∴$MQ=\frac{m}{2}$,
∴DQ=m,
∴$S=\frac{1}{2}{m}^{2}$;
(3)①当点P运动到点(2,0)时,N点与B点重合,
此时,OP=2,NP=2,AQ=4,Q(6,0),HP=2$\sqrt{2}$,$MQ=\frac{1}{4}AQ=1$,
∴$\frac{NP}{MQ}=2$,
过点N作NT⊥HP于点T,如图2,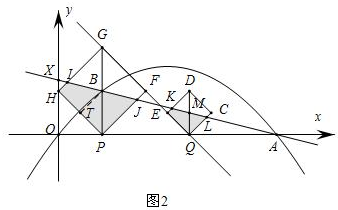
则$NT=\sqrt{2}$,
∴S梯IHPJ=NT×HP=4,
∵梯形IHPJ与梯形KEQL相似,相似比为$\frac{NP}{MQ}=2$,
∴${S}_{梯KEQL}=\frac{1}{4}{S}_{梯IHPJ}$=1,
∴S阴=S梯IHPJ+S梯KEQL=5;
②当点P运动到点(2,0)时,延长DE交x轴于点R,如图3,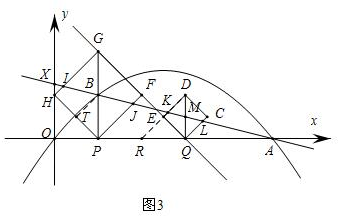
此时,PR=2,
接着,点P与点R相向运动至重合时,DE与PF重合,同时CD与GF重合,
由于始终有AQ=2OP,由题意M(10-2m,$\frac{1}{2}$m).此时OP+RQ+AQ=10,
m+m+2m=10,
m=$\frac{5}{2}$
此时P点坐标为($\frac{5}{2}$,0);
当P点与Q点继续相向运动至相遇时,HP与EQ,QC与PF均重合,
对于整个全程OA=10而言,P点运动的路程为$\frac{1}{3}×10=\frac{10}{3}$,
即P、Q相遇时,P点的坐标为($\frac{10}{3}$,0);
综上所述,当P点坐标为($\frac{8}{3}$,0)、($\frac{10}{3}$,0)时,会出现两个正方形分别有边落在同一条直线上.
点评 本题考查了待定系数法求二次函数解析式、待定系数法求一次函数解析式、相似三角形的判定与性质、正方形的面积计算、梯形的面积计算、动点相遇问题等知识点,有一定综合性,难度适中.对于第(2)问,知道两个梯形相似是关键;第(3)问只要将问题转化为点的相遇问题就很容易解决,化归与转化的数学思想一直是考查的重点,要引起重视.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 105度 | B. | 125度 | C. | 150度 | D. | 160度 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
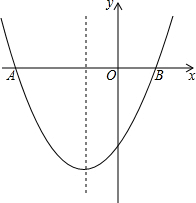 已知:抛物线y=ax2+bx+c(a≠0)的对称轴为x=-2,与x轴交于A、B两点,与y轴交于点C,其中A(-6,0),C(0,-4).
已知:抛物线y=ax2+bx+c(a≠0)的对称轴为x=-2,与x轴交于A、B两点,与y轴交于点C,其中A(-6,0),C(0,-4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
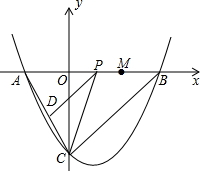 已知:如图,抛物线y=a(x-1)2+c与y轴交于点C(0,-4),与x轴交于点A、B,点A的坐标为(-2,0).
已知:如图,抛物线y=a(x-1)2+c与y轴交于点C(0,-4),与x轴交于点A、B,点A的坐标为(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
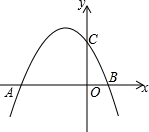 如图,抛物线y=-$\frac{3}{8}{x}^{2}-\frac{3}{4}x+3$与x轴交于A,B两点,与y轴交于点C.
如图,抛物线y=-$\frac{3}{8}{x}^{2}-\frac{3}{4}x+3$与x轴交于A,B两点,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
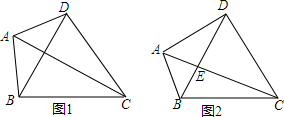
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
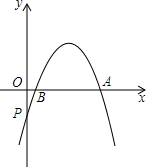 已知二次函数y=ax2+bx+c的图象经过点P(0,$-\frac{5}{2}$)、A(5,0)、B(1,0).
已知二次函数y=ax2+bx+c的图象经过点P(0,$-\frac{5}{2}$)、A(5,0)、B(1,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com