
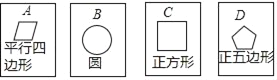
【题目】在四张背面完全相同的纸牌A、B、C、D中,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张(不放回),再从余下的3张纸牌中摸出一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-4,2)、B(0,4)、C(0,2),
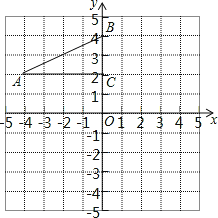
(1)画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
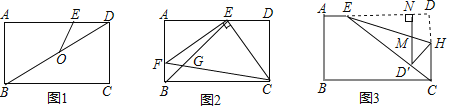
【题目】如图,在矩形ABCD中,AB=3,BC=5,E是AD上的一个动点.
(1)如图1,连接BD,O是对角线BD的中点,连接OE.当OE=DE时,求AE的长;
(2)如图2,连接BE,EC,过点E作EF⊥EC交AB于点F,连接CF,与BE交于点G.当BE平分∠ABC时,求BG的长;
(3)如图3,连接EC,点H在CD上,将矩形ABCD沿直线EH折叠,折叠后点D落在EC上的点D'处,过点D′作D′N⊥AD于点N,与EH交于点M,且AE=1.
①求![]() 的值;
的值;
②连接BE,△D'MH与△CBE是否相似?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
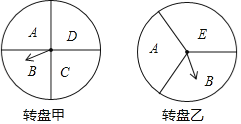
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受9折优惠的概率为多少;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 中,
中,![]() ,
,![]() 与
与![]() 交于
交于![]() ,
,![]() 为
为![]() 延长线上的一点,且
延长线上的一点,且![]() ,连结
,连结![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() 则下列结论:①
则下列结论:①![]() ;②与
;②与![]() 全等的三角形共有
全等的三角形共有![]() 个;③
个;③![]() ;④由点
;④由点![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形是菱形.其中正确的是( )
构成的四边形是菱形.其中正确的是( )

A.①④B.①③④C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店如果将进货价为8元的商品按每件10元售出,每天可销售200件,现在采用提高售价,减少进货量的方法增加利润,已知这种商品每涨价0.5元,其销量就减少10件.
(1)要使每天获得利润700元,请你帮忙确定售价;
(2)问售价定在多少时能使每天获得的利润最多?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)分别求出该反比例函数和直线AB的解析式;
(2)求出交点D坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
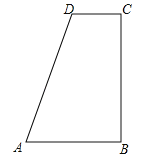
【题目】如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.
(1)利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法);
(2)在(1)的条件下,①证明:AE⊥DE;
②若CD=2,AB=4,点M,N分别是AE,AB上的动点,求BM+MN的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com