
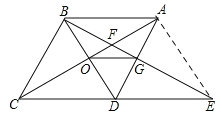
【题目】如图,菱形![]() 中,
中,![]() ,
,![]() 与
与![]() 交于
交于![]() ,
,![]() 为
为![]() 延长线上的一点,且
延长线上的一点,且![]() ,连结
,连结![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() 则下列结论:①
则下列结论:①![]() ;②与
;②与![]() 全等的三角形共有
全等的三角形共有![]() 个;③
个;③![]() ;④由点
;④由点![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形是菱形.其中正确的是( )
构成的四边形是菱形.其中正确的是( )

A.①④B.①③④C.①②③D.②③④
【答案】A
【解析】
连结![]() ,可说明四边形
,可说明四边形![]() 是平行四边形,即
是平行四边形,即![]() 是
是![]() 的中点;由有题意的可得O是BD的中点,即可判定①;运用菱形和平行四边形的性质寻找判定全等三角形的条件,找出与其全等的三角形即可判定②;证出OG是△ABD的中位线,得出OG//AB,OG=
的中点;由有题意的可得O是BD的中点,即可判定①;运用菱形和平行四边形的性质寻找判定全等三角形的条件,找出与其全等的三角形即可判定②;证出OG是△ABD的中位线,得出OG//AB,OG=![]() AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形0DGF=S△ABF.即可判定③;先说明△ABD是等边三角形,则BD=AB,即可判定④.
AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形0DGF=S△ABF.即可判定③;先说明△ABD是等边三角形,则BD=AB,即可判定④.
解:如图:连结![]() .
.
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 是
是![]() 的中点,
的中点,
∵O是BD的中点
![]() ,①正确;
,①正确;
有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共
,共![]() 个,②错误;
个,②错误;
∵OB=OD,AG=DG,
∴OG是△ABD的中位线,
∴OG//AB,OG=![]() AB,
AB,
∴△GOD∽△ABD,△ABF∽△OGF,
∵△GOD的面积=![]() △ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
∴△AFG的面积=△OGF的面积的2倍,
又∵△GOD的面积=△A0G的面积=△B0G的面积,
.∴![]() ;不正确;③错误;
;不正确;③错误;
![]()
![]() 是等边三角形.
是等边三角形.
![]() ,
,
![]() 是菱形,④正确.
是菱形,④正确.
故答案为A.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC=8,点D在△ABC外,连接AD、BD,且∠ADB=90°,AB、CD相交于点E,AB、CD的中点分别是点F、G,连接FG.

(1)求AB的长;
(2)求证:AD+BD=![]() CD;
CD;
(3)若BD=6,求FG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象经过点A(1,3).
的图象经过点A(1,3).
(1)试确定此反比例函数的解析式;
(2)当![]() =2时, 求y的值;
=2时, 求y的值;
(3)当自变量![]() 从5增大到8时,函数值y是怎样变化的?
从5增大到8时,函数值y是怎样变化的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABO的面积为8,OA=OB,BC=12,点P的坐标是(a,6).
(1) △ABC三个顶点的坐标分别为A( , ),B( , ),C( , );
(2) 是否存在点P,使得![]() ?若存在,求出满足条件的所有点P的坐标.
?若存在,求出满足条件的所有点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4﹣7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将这四类的人数绘制成扇形图(如图1)和条形图(如图2).
经确认扇形图是正确的,而条形图尚有一处错误.
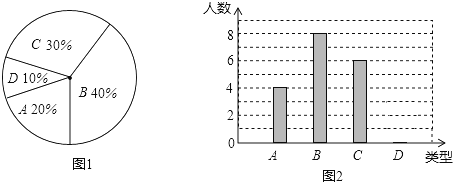
回答下列问题:
(1)写出条形图中存在的错误为________;
(2)写出这20名学生每人植树量的众数为________;中位数为________;
(3)经计算这20名学生每人植树量的平均数为5.3,则估算这260名学生共植树________棵;
(4)在这次活动中,九(1)班学生平均每人植6棵树,如果单独由男同学完成,每人应植树15棵,求如果单独由女同学完成,每人应植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.

(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与t的变化规律,写出y1与t的函数关系式及自变量t的取值范围;
(2)分别探求该产品在国外市场上市20天前(不含第20天)与20天后(含第20天)的日销售量y2与时间t所符合的函数关系式,并写出相应自变量t的取值范围;
(3)设国内、外市场的日销售总量为y万件,写出y与时间t的函数关系式,并判断上市第几天国内、外市场的日销售总量y最大,并求出此时的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知代数式(ax-3)(2x+4)-x2-b化简后,不含x2项和常数项.
(1)求a,b的值;
(2)求(2a+b)2-(a-2b)(a+2b)-3a(a-b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不低于270万元,又不超过296万元.开发建设办公室预算:一套A型“廉租房”的造价为10万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2) 在投入资金最少的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低1万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com