Question

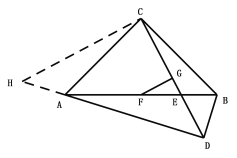
【题目】如图，在等腰Rt△ABC中，∠ACB=90°，AC=BC=8，点D在△ABC外，连接AD、BD，且∠ADB=90°，AB、CD相交于点E，AB、CD的中点分别是点F、G，连接FG．

（1）求AB的长；

（2）求证：AD+BD=CD；

（3）若BD=6，求FG的值．

Answer 1

【答案】（1）；（2）见解析；（3）

【解析】

(1)运用勾股定理即可求得AB的长；

（2）过点C作CH⊥CD，交DA的延长线于点H，然后再说明△ACH≌△BCD，最后利用勾股定理和线段的和差即可证明；

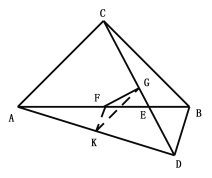
（3）取AD的中点K，连接FK、KG，进而说明FK、GK分别是△ABD、△DAC的中位线即可求得FK、GK的长；连接FD，由第（2）得AD+BD=CD；连接CF，可知；最后利用勾股定理解答即可．

（1）解：在Rt△ABC中

∴AB===

（2）过点C作CH⊥CD，交DA的延长线于点H

∵∠ACB=90°，∠ADB=90°

∴∠CAD+∠CBD=360°-90°-90°=180°

∵∠CAD+∠CAH=180°

∴∠CBD=∠CAH

∵CH⊥CD，∠ACB=90°

∴∠ACH=∠BCD=90°-∠ACE

∵CA=CB

∴△ACH≌△BCD（ASA）

∴CH=CD，AH=DB

在Rt△HCD中

∴DH===

∴AD+BD=AD+AH=DH=CD．

（3）解：取AD的中点K，连接FK、KG

∵K、F、G分别是AD、AB、CD的中点

∴FK、GK分别是△ABD、△DAC的中位线

∴，

在△FGK中，GK-FK<FG<GK+FK，即4-3<FG<4+3，

∴1<FG<7．

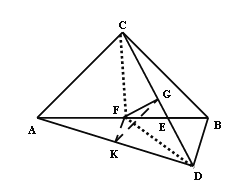
连接FD，由第（2）的：AD+BD=CD

∴，∴

又

连接CF，可知

∴CF=DF

∴FG⊥CD

在Rt△FGD中，

=．