
【题目】如图,![]() 是边长
是边长![]() 的等边三角形,动点
的等边三角形,动点![]() 、
、![]() 同时从
同时从![]() 、
、![]() 两点出发,分别在
两点出发,分别在![]() 、
、![]() 边上匀速移动,它们的速度分别为
边上匀速移动,它们的速度分别为![]() ,
,![]() ,当点
,当点![]() 到达点
到达点![]() 时,P、Q两点停止运动,设点
时,P、Q两点停止运动,设点![]() 的运动时间为
的运动时间为![]() ,则当
,则当![]() =_____
=_____![]() 时,
时,![]() 为直角三角形.
为直角三角形.

科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() 的图象相交于A、B两点,以AB为边,在直线AB的左侧作菱形ABCD,边BC⊥y轴于点E,若点A坐标为(m,6),tan∠BOE=
的图象相交于A、B两点,以AB为边,在直线AB的左侧作菱形ABCD,边BC⊥y轴于点E,若点A坐标为(m,6),tan∠BOE=![]() ,OE=
,OE=![]() .
.

(1)求反比例函数和一次函数的解析式;
(2)求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:ABC平移后得出△A1B1C1,点A(﹣1,3)平移后得A1(﹣4,2),又已知B1(﹣2,3),C1(1,﹣1),求B、C坐标,画图并说明经过了怎样的平移.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.

(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )

A.8m B.6.4m C.4.8m D.10m
【答案】A.
【解析】
试题分析:因为人和树均垂直于地面,所以和光线构成的两个直角三角形相似,
设树高x米,则![]() ,即
,即![]() ,解得,x=8. 故选A.
,解得,x=8. 故选A.
考点:相似三角形的应用.
【题型】单选题
【结束】
11
【题目】已知圆锥的底面半径为1cm,母线长为3cm,则其全面积为________cm2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,完成下列推理过程:
如图所示,点E在![]() 外部,点D在BC边上,DE交AC于F,若
外部,点D在BC边上,DE交AC于F,若![]() ,
,![]() ,
,
求证:![]() .
.

证明:∵![]() (已知),
(已知),
![]() (________________),
(________________),
∴![]() (________________),
(________________),
又∵![]() ,
,
∴________![]() ________
________![]() (________),
(________),
即![]() ,
,
在![]() 和
和![]() 中
中
![]() (已证)
(已证)
∵![]() (已知)
(已知)
![]() (已证)
(已证)
∴![]() (________).
(________).
∴![]() (________________)
(________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
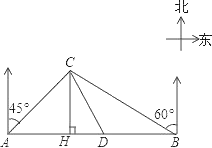
【题目】某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
(1)求牧民区C到B地的距离(结果用根式表示);
(2)一天,乙医疗队的医生要到牧民区C出诊,她先由B地搭车沿公路AB到D处(BD<AB)转车,再由D地沿DC方向到牧民区C.若C、D两地距离是B、C两地距离的![]() 倍,求B、D两地的距离.(结果精确到0.1千米 参考数据:
倍,求B、D两地的距离.(结果精确到0.1千米 参考数据: ![]() ≈2.449,
≈2.449, ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com