
【题目】某商店销售甲、乙两种商品,现有如下信息: 请结合以上信息,解答下列问题:
(1)求甲、乙两种商品的进货单价;
(2)已知甲、乙两种商品的零售单价分别为2元、3元,该商店平均每天卖出甲商品500件和乙商品1300件,经市场调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件,商店决定把甲种商品的零售单价下降m(m>0)元,在不考虑其他因素的条件下,求当m为何值时,商店每天销售甲、乙两种商品获取的总利润为1800元(注:单件利润=零售单价﹣进货单价)
【答案】
(1)解:设甲商品进货单价x元,乙商品进货单价y元.
依题意,得
![]()
解得: ![]() .
.
答:甲商品进货单价为1元,乙商品进货单价为2元
(2)解:依题意,得
(2﹣m﹣1)(500+1000m)+(3﹣2)×1300=1800
(1﹣m)(500+1000m)=500
即2m2﹣m=0
∴m1=0.5,m2=0
∵m>0
∴m=0不合舍去,即m=0.5
答:当m=0.5时,商店获取的总利润为1800元
【解析】(1)根据图上信息可以得出甲乙商品之间价格之间的等量关系,即可得出方程组求出即可;(2)根据降价后甲每天卖出:(500+ ![]() ×100)件,每件降价后每件利润为:(1﹣m)元;即可得出总利润,利用一元二次方程解法求出即可.
×100)件,每件降价后每件利润为:(1﹣m)元;即可得出总利润,利用一元二次方程解法求出即可.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为cm. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC的两边分别平行于∠DEF的两边,且∠ABC=25°.
(1)∠1=________________,∠2=________________;
(2)请观察∠1、∠2分别与∠ABC有怎样的关系,归纳出一个命题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE. 
(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点P是不等边△ABC的边BC上的一点,点D在边AB或AC上,若由点P、D截得的小三角形与△ABC相似,那么D点的位置最多有( ) 
A.2处
B.3处
C.4处
D.5处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O. 
(1)连接AF,CE,求证:四边形AFCE为菱形;
(2)求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y= ![]() (k>0)上,则k的值为( )
(k>0)上,则k的值为( )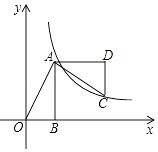
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com