
【题目】如图,∠ABC的两边分别平行于∠DEF的两边,且∠ABC=25°.
(1)∠1=________________,∠2=________________;
(2)请观察∠1、∠2分别与∠ABC有怎样的关系,归纳出一个命题.

【答案】(1)25°;155°(2)命题:如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.
【解析】
(1)图1,根据平行线的性质,由AB∥DE得到∠B=∠DGC=25°,再由BC∥EF得∠1=∠DGC=25°;图2,根据平行线的性质,由AB∥DE得∠B=∠BGE=25°,再由BC∥EF得∠2+∠BGE=180°,所以∠2=155°;
(2)由(1)的计算结果易得∠1与∠ABC相等,∠2与∠ABC互补,这个结论可归纳为:如果两个角的两边分别平行,那么这两个角相等或互补.
解:(1)图1,∵AB∥DE,
∴∠B=∠DGC=25°,
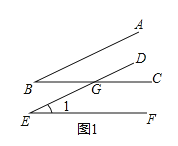
∵BC∥EF,
∴∠1=∠DGC=25°;
图2,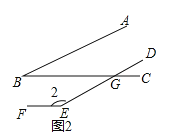
∵AB∥DE,
∴∠B=∠BGE=25°,
∵BC∥EF,
∴∠2+∠BGE=180°,
∴∠2=180°-25°=155°;
故答案为25°,155°;
(2)∠1与∠ABC相等,∠2与∠ABC互补,
结论:如果两个角的两边分别平行,那么这两个角相等或互补.


科目:初中数学 来源: 题型:
【题目】在直角梯形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm。点P从点A出发,以每秒3cm的速度沿折线ABCD运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动。已知动点P,Q同时出发,当点Q运动到点C时,P,Q运动停止,设运动时间为t秒.
(1)求CD的长.
(2)t为何值时?四边形PBQD为平行四边形.
(3)在点P,点Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 90 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H. 
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.求证:△AGE≌△AFE; 
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲同学用图3-①所示的方法作出了点C,表示数![]() ,在△OAB中,∠OAB=90°,OA=2,AB=3,且点O,A,C在同一数轴上,OB=OC.
,在△OAB中,∠OAB=90°,OA=2,AB=3,且点O,A,C在同一数轴上,OB=OC.
(1)请说明甲同学这样做的理由;
(2)仿照甲同学的作法,在图3-②所给的数轴上描出表示-![]() 的点A.
的点A.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点P是BC的中点,仅用无刻度的直尺按要求画图:
(1)在图①中画出AD的中点M; 
(2)在图②中画出对角线AC的三等分点E,点F. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售甲、乙两种商品,现有如下信息: 请结合以上信息,解答下列问题:
(1)求甲、乙两种商品的进货单价;
(2)已知甲、乙两种商品的零售单价分别为2元、3元,该商店平均每天卖出甲商品500件和乙商品1300件,经市场调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件,商店决定把甲种商品的零售单价下降m(m>0)元,在不考虑其他因素的条件下,求当m为何值时,商店每天销售甲、乙两种商品获取的总利润为1800元(注:单件利润=零售单价﹣进货单价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,AD是∠BAC的平分线.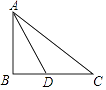
(1)尺规作图:过点D作DE⊥AC于E;
(2)求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com