
����Ŀ����ֱ������ABCD�У�AB��CD����BCD=90�㣬AB=AD=10cm��BC=8cm����P�ӵ�A��������ÿ��3cm���ٶ�������ABCD�˶�����Q�ӵ�D��������ÿ��2cm���ٶ����߶�DC�������C�˶�����֪����P��Qͬʱ����������Q�˶�����Cʱ��P��Q�˶�ֹͣ�����˶�ʱ��Ϊt��.
��1����CD�ij�.
��2��tΪ��ֵʱ���ı���PBQDΪƽ���ı���.
��3���ڵ�P����Q���˶������У��Ƿ����ijһʱ�̣�ʹ����BPQ�����Ϊ20cm2�������ڣ��������������������t��ֵ���������ڣ���˵������.

���𰸡���1��16����2��![]() ����3��
����3��![]() .
.
�������������������1������A��AM��CD��M���ı���AMCB�Ǿ��Σ�AM=BC,AD����֪�ģ����ݹ��ɶ������DM,CM=AB,����CD��������ˣ���2�����ı���PBQDΪƽ���ı���ʱ,��P��AB�ϣ���Q��DC�ϣ���t��ʾ��BP,DQ�ij�������BP=DQ,���tֵ����BP,DQ���������Ȼ�����CQ,�ù��ɶ������BQ���ı���PBQD���ܳ���������ˣ���3��D��Q��C��Ҫ8�룬����t�ķ�Χ��0��t��8,Q����P�����߶β�ͬ��������������ۣ���������P���߶�AB��ʱ����![]() ʱ����t��ʾ��BP�ij�����������BPQ���������20�ķ�����⣻������P���߶�BC��ʱ����
ʱ����t��ʾ��BP�ij�����������BPQ���������20�ķ�����⣻������P���߶�BC��ʱ����![]() ʱ����t��ʾ��BP,CQ�ij�������������BPQ���������20�ķ�����⣻������P���߶�CD��ʱ����Ϊ����������ʱ����
ʱ����t��ʾ��BP,CQ�ij�������������BPQ���������20�ķ�����⣻������P���߶�CD��ʱ����Ϊ����������ʱ����![]() ������P��Q���Ҳ࣬��6��t��
������P��Q���Ҳ࣬��6��t��![]() ����t��ʾ��PQ�ij��������г��������ʽ��⣻����P��Q����࣬��
����t��ʾ��PQ�ij��������г��������ʽ��⣻����P��Q����࣬��![]() ����t��ʾ��PQ�ij����г��������ʽ��⣮
����t��ʾ��PQ�ij����г��������ʽ��⣮
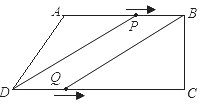
�����������1������A��AM��CD��M�����ݹ��ɶ�����AD=10��AM=BC=8����DM=![]() =6����CD=16����2�����ı���PBQDΪƽ���ı���ʱ����P��AB�ϣ���Q��DC�ϣ���ͼ������֪��AP=3t,BP=10��3t��DQ=2t����10��3t=2t�����t=2����ʱ��BP=DQ=4��CQ=12����
=6����CD=16����2�����ı���PBQDΪƽ���ı���ʱ����P��AB�ϣ���Q��DC�ϣ���ͼ������֪��AP=3t,BP=10��3t��DQ=2t����10��3t=2t�����t=2����ʱ��BP=DQ=4��CQ=12����![]() �����ı���PBQD���ܳ�=2��BP+BQ��=
�����ı���PBQD���ܳ�=2��BP+BQ��=![]() ��
��
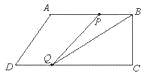
��3��������P���߶�AB��ʱ����B��ʱ��![]() �룬��
�룬��![]() ʱ����ͼ��BP=10��3t��BC=8����
ʱ����ͼ��BP=10��3t��BC=8����![]() ����
����![]() ��
��
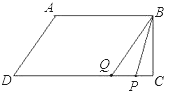
������P���߶�BC��ʱ��P����C��tֵʱ6�룬��![]() ʱ����ͼ��BP=AB+BP-AB=3t��10��DQ=2t,CQ=16��2t����
ʱ����ͼ��BP=AB+BP-AB=3t��10��DQ=2t,CQ=16��2t����![]() ������ã�3t2��34t+100=0����=��44��0�����Է�����ʵ���⣮�������������������BPQ�������20��
������ã�3t2��34t+100=0����=��44��0�����Է�����ʵ���⣮�������������������BPQ�������20��

������P���߶�CD��ʱ��P����Q������ʱ,����2t+3t=10+8+16,t=![]() ,����ʱ����
,����ʱ����![]() ������P��Q���Ҳ࣬��6��t��
������P��Q���Ҳ࣬��6��t��![]() ������PQ=34-��2t+3t��=34��5t������
������PQ=34-��2t+3t��=34��5t������![]() ����˷��̵ã�
����˷��̵ã�
![]() ��6����ȥ������P��Q����࣬��
��6����ȥ������P��Q����࣬��![]() ������PQ=2t+3t-34=5t��34�����з��̣�
������PQ=2t+3t-34=5t��34�����з��̣�![]() ����ã�t=7��8�����ۺϵó�����������tֵ���ڣ���ֵ�ֱ�Ϊ
����ã�t=7��8�����ۺϵó�����������tֵ���ڣ���ֵ�ֱ�Ϊ![]() ��t2=7��8��
��t2=7��8��


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�������ع���ij������ˮ����ο��ҽ�����ߣ������ضԹ�������3000ǧ�����ϣ���3000ǧ�ˣ������������۷�����������ÿǧ��9Ԫ���ɻ����ͻ����ţ��ҷ�����ÿǧ��8Ԫ���ɹ˿��Լ���˻أ���֪�ù�˾��ӻ��ص���˾�������Ϊ5000Ԫ��
(1)�ֱ�д���ù�˾���ֹ����ĸ���y��Ԫ�����������ˮ������x��ǧ�ˣ�֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
(2)���ݹ������жϣ�ѡ�����ֹ����������٣���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�BI��CI�ֱ�ƽ�֡�ABC����ACB����I����DE��BC����AB��D����AC��E���������н��ۣ��١�DBI�ǵ��������Σ��ڡ�ACI�ǵ��������Σ���AIƽ�֡�BAC���ܡ�ADE�ܳ�����AB��AC.������ȷ����(����)

A. �٢ڢ� B. �ڢۢ� C. �٢ۢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�D��ֱ����AD�С�D�ڵ�A��EC=CB�������н��ۣ���BA��DA�� ��OC��AE���ۡ�COE=2��CAE����OD��AC��һ����ȷ�ĸ����У� ��
A.4��
B.3��
C.2��
D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D�ڵȱߡ�ABC�ı�BC�ϣ� 
��1���ѡ�ACD�Ƶ�A˳ʱ����ת��ʹ��C���B�غϣ�������ת��ġ�ABD�䣻
��2�����AC=4��CD=1����1���е�D��ת���߹���·�̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����ҹ���x��һԪ���η���ax2+bx+c��m=0����������ȵ�ʵ���������н��ۣ� ��b2��4ac��0����abc��0����a��b+c��0����m����2��
���У���ȷ�ĸ����У� ��
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ŵȱ�������ֽƬ����λ����4��С�����Σ���Ϊ��һ�β�����Ȼ�����е�һ�������ΰ�ͬ����ʽ�ټ���4��С�����Σ����õ�7��С�����Σ���Ϊ�ڶ��β������ٽ�����һ�������ΰ�ͬ����ʽ�ټ���4��С�����Σ����õ�10��С�����Σ���Ϊ�����β��������������ϲ�������Ҫ�õ�100��С�����Σ�����Ҫ�����Ĵ����� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=5cm��BC=12cm������ABC�Ƶ�B˳ʱ����ת60�㣬�õ���BDE������DC��AB�ڵ�F�����ACF���BDF���ܳ�֮��Ϊcm�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�����߷ֱ�ƽ���ڡ�DEF�����ߣ��ҡ�ABC��25��.
(1)��1��________________����2��________________��
(2)��۲��1����2�ֱ����ABC�������Ĺ�ϵ�����ɳ�һ�����⣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com