
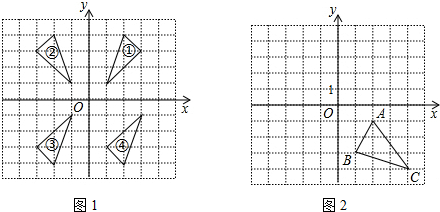
分析 (1)利用轴对称图形以及关于原点对称图形的性质进而分析得出答案;
(2)利用关于原点对称点的性质得出对应点位置进而得出答案,再利用△A1B1C1所在矩形面积减去周围三角形面积进而得出答案.
解答 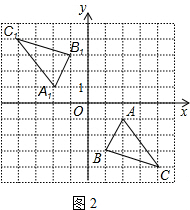 解:(1)如图所示:关于y轴对称的两个三角形的编号为:①②,
解:(1)如图所示:关于y轴对称的两个三角形的编号为:①②,
关于坐标原点O对称的两个三角形的编号为:①③;
故答案为:①②;①③;
(2)如图所示:△A1B1C1即为所求;
△A1B1C1的面积为:3×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×3=3.5.
点评 此题主要考查了旋转变换以及轴对称变换和三角形面积求法,根据题意得出对应点位置是解题关键.


科目:初中数学 来源: 题型:解答题
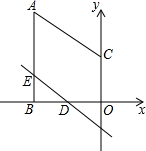 如图在平面直角坐标系内,点A与点C的坐标分别为(-4,8),(0,5),过点A作AB⊥x轴于点B,过OB上的动点D作直线y=kx+b平行于AC,与AB相交于点E,连结CD,过点E作直线EF∥CD,交AC于点F.
如图在平面直角坐标系内,点A与点C的坐标分别为(-4,8),(0,5),过点A作AB⊥x轴于点B,过OB上的动点D作直线y=kx+b平行于AC,与AB相交于点E,连结CD,过点E作直线EF∥CD,交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50(1+x)=72 | B. | 50(1+x)+50(1+x)2=72 | C. | 50(1-x)2=72 | D. | 72(1-x)2=50 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 长度相等的弧是等弧 | |
| B. | 等弧必须是同圆或等圆中的弧,否则不能互相重合 | |
| C. | 度数相等的弧不一定是等弧 | |
| D. | 等弧的度数相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A是100°第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A是100°第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{2}$ | B. | $\frac{a}{3}$ | C. | $\frac{a}{4}$ | D. | 以上结果都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.395≤a<1.405 | B. | 1.35≤a<1.45 | C. | 1.30<a<1.50 | D. | 1.400≤a<1.405 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com