
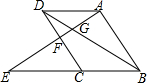
 如图,?ABCD,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=2,GF=1,则EF=3.
如图,?ABCD,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=2,GF=1,则EF=3. 分析 运用平行四边形的性质证明△ADG∽△EBG,△DGF∽△BGA,得出比例式,得出AG2=EG•FG,代入数值即可得出结果.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BE,AB∥DF;
∴△ADG∽△EBG,△DGF∽△BGA,
∴$\frac{AG}{EG}$=$\frac{DG}{BG}$,$\frac{FG}{AG}$=$\frac{DG}{BG}$,
∴$\frac{AG}{EG}$=$\frac{FG}{AG}$,
∴AG2=EG•FG,
∴22=(EF+1)×1,
解得:EF=3,
故答案为:3.
点评 本题考查了平行四边形的性质、相似三角形的判定及其性质等知识;熟练掌握平行四边形的性质,由三角形相似得出比例式是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
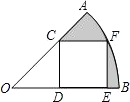 如图,在半径为$\sqrt{10}$,圆心角等于45°的扇形AOB内部作一个正方形CDEF,使点C在OA上,点D、E在OB上,点F在弧AB上,则阴影部分的面积为$\frac{5π}{4}$-3.(结果保留π)
如图,在半径为$\sqrt{10}$,圆心角等于45°的扇形AOB内部作一个正方形CDEF,使点C在OA上,点D、E在OB上,点F在弧AB上,则阴影部分的面积为$\frac{5π}{4}$-3.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com