Question

【题目】如图，已知、，，为点关于的对称点，反比例函数的图像经过点．

（）证明四边形为菱形．

（）求此反比例函数的解析式．

（）已知点在的图像上，点在轴上，且点、、、组成四边形是平行四边形，求点的坐标．

Answer 1

【答案】（）证明见解析（）（）点的坐标为，，

【解析】

试题（）先计算出，，再根据轴对称的性质得，，于是可根据菱形的判定方法得到四边形为菱形；

（）由菱形的性质得，则，然后把点坐标代入关系式求出的值即可得到反比例函数解析式；

（）讨论：当为对角线，利用平行四边形的性质，可把点向右平移个单位可得点，则点向右平移个单位可得点，则利用反比例函数解析式可确定坐标，于是得到点通过平移可得点，利用同样平移得到点坐标，当为边，由四边形为平行四边形得到，，则可确定坐标，进而可求，及，易得点坐标．

试题解析：（）∵、，，

∴，，

∵为点关于的对称点，

∴，，

∴，

∴四边形为菱形．

（）∵四边形为菱形，

∴，

而，，

∴，

把代入得，

∴反比例函数解析式为．

（）当为对角线，如图，

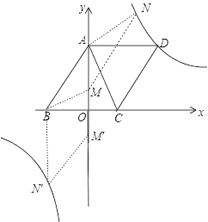
∵四边形为平行四边形，

∴点向右平移个单位可得点，点向右平移个单位可得点，

∴点的横坐标为，

当时，，则，

∴点向右平移个单位，再向上平移单位可得点，

∴点向右平移个单位可得点，再向上平移单位可得点，此时点坐标为；

当为边，

∵四边形为平行四边形，

∴，，

∴点的横坐标为，则，

∴，

∴，或，

此时点坐标为或，

综上所述，满足条件的点的坐标为，，．