
【题目】已知关于方程x 的一元二次方程x2﹣2(k﹣1)x﹣k2﹣1=0.
(1)求证:此方程总有两个不相等的实数根;
(2)如果方程的两实数根满足x12+x22=4,求k的值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】将一副三角尺(在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() )如图摆放,点
)如图摆放,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形,剩余部分折成一个无盖的盒子.(纸板的厚度忽略不计).
(1)若该无盖盒子的底面积为900cm2,求剪掉的正方形的边长;
(2)求折成的无盖盒子的侧面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,河流两岸PQ,MN互相平行,C、D是河岸PQ上间隔50m的两个电线杆,某人在河岸MN上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=70°,求河流的宽度(结果精确到个位,![]() =1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
=1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
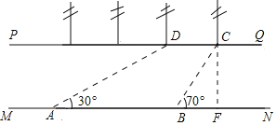
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③abc>0;④b2+8a>4ac.其中正确的有( )
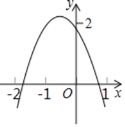
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示折叠,使点D与点O重合,折痕为FG,点F、G分别在AD,BC上,连接OG、DG,若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是
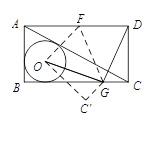
A.CD+DF=4B.CDDF=2![]() 3
3
C.BC+AB=2![]() +4D.BCAB=2
+4D.BCAB=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
请解答下列问题:
(1)画出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() ,并直接写出
,并直接写出![]() 点的坐标;
点的坐标;
(2)以原点![]() 为位似中心,位似比为1:2,在
为位似中心,位似比为1:2,在![]() 轴的右侧,画出
轴的右侧,画出![]() 放大后的图形
放大后的图形![]() ,并直接写出
,并直接写出![]() 点的坐标;
点的坐标;
(3)如果点![]() 在线段
在线段![]() 上,请直接写出经过(2)的变化后对应点
上,请直接写出经过(2)的变化后对应点![]() 的坐标.
的坐标.
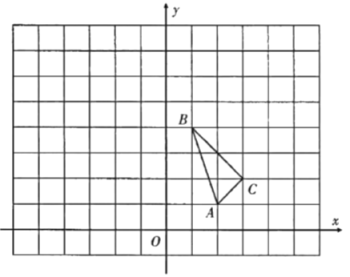
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE是两个不全等的等腰直角三角形,其中点B与点D是直角顶点,现固定△ABC,而将△ADE绕点A在平面内旋转.
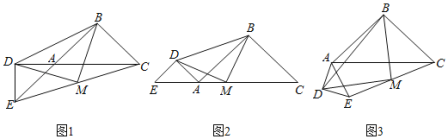
(1)如图1,当点D在CA延长线上时,点M为EC的中点,求证:△DMB是等腰三角形.
(2)如图2,当点E在CA延长线上时,M是EC上一点,若△DMB是等腰直角三角形,∠DMB为直角,求证:点M是EC的中点.
(3)如图3,当△ADE绕点A旋转任意角度时,线段EC上是否都存在点M,使△BMD为等腰直角三角形,若不存在,请举出反例;若存在,请予以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com