
【题目】如图,△ABC和△ADE是两个不全等的等腰直角三角形,其中点B与点D是直角顶点,现固定△ABC,而将△ADE绕点A在平面内旋转.
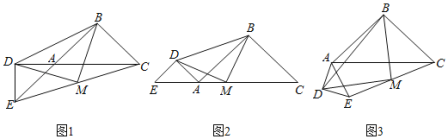
(1)如图1,当点D在CA延长线上时,点M为EC的中点,求证:△DMB是等腰三角形.
(2)如图2,当点E在CA延长线上时,M是EC上一点,若△DMB是等腰直角三角形,∠DMB为直角,求证:点M是EC的中点.
(3)如图3,当△ADE绕点A旋转任意角度时,线段EC上是否都存在点M,使△BMD为等腰直角三角形,若不存在,请举出反例;若存在,请予以证明.
【答案】(1)见解析;(2)见解析;(3)线段EC上都存在中点M,使△BMD为等腰直角三角形,理由见解析
【解析】
(1)利用直角三角形斜边上的中线等于斜边的一半得出BM=DM=![]() EC,即可得出答案;
EC,即可得出答案;
(2)根据AAS证明△DFM≌∠MGB,得FM=BG,DF=MG,根据线段的和表示EM和MC,可得结论;
(3)线段EC上都存在中点M,使△BMD为等腰直角三角形,作辅助线,构建全等三角形,证明△DFM≌∠MGB(SAS),得BM=DM,∠FMD=∠GBM,再证明∠DMB=90°,可得结论.
(1)如图1,∵∠EDC=90°,点M为EC的中点,
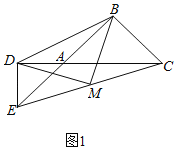
∴DM=![]() EC.
EC.
同理可得:BM=![]() EC.
EC.
∴DM=BM,
∴△DMB是等腰三角形;
(2)过点D作DF⊥EA,过点B作BG⊥AC,
∵△ABC和△ADE是两个等腰直角三角形,
∴BG=GC=AG,DF=EF=FA,
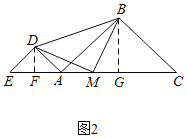
∴∠DFM=∠BGM=90°,
∴∠FDM+∠DMF=90°,
∵△DMB是等腰直角三角形,
∴DM=BM,∠DMB=90°,
∴∠BMG+∠DMF=90°,
∴∠FDM=∠BMG,
∴△DFM≌∠MGB(AAS),
∴FM=BG,DF=MG,
∵BG=GC,DF=EF,
∴FM=GC,MG=EF,
∵EM=EF+FM,MC=MG+GC,
∴EM=MC,
∴点M是EC的中点;
(3)线段EC上都存在中点M,使△BMD为等腰直角三角形,
理由是:取AE中点F,AC中点G,连接FD,FM,BG,GM,
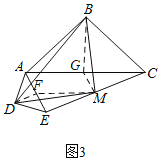
∵点M是EC的中点,点G是AC的中点,
∴GM=![]() AE,GM∥AE,BG⊥AC,∠BGC=90
AE,GM∥AE,BG⊥AC,∠BGC=90![]() ,
,
∵F是AE中点,
∴AF=![]() AE,DF⊥AE,∠DFE=90
AE,DF⊥AE,∠DFE=90![]() ,
,
∴AF∥GM,AF=GM,
∴四边形AFMG是平行四边形,
∴∠AFM=∠AGM,
∴∠EFM=∠MGC.
∵∠DFM=∠EFM+∠DFE=∠EFM+90![]() ,
,
∠BGM=∠MGC+∠BGC=∠MGC+90![]() ,
,
∴∠DFM=∠BGM,
∵GM=AF=DF,
∴DF=GM,
同理可得 BG=FM,
∴△DFM≌∠MGB(SAS),
∴BM=DM,∠FMD=∠GBM,
∵FM∥AC,
∴∠FMG=∠CGM,
∴∠DMB=∠FMD+∠FMG+∠GMB,
=∠GBM+∠CGM+∠GMB,
=180°﹣∠BGC,
=90°,
∴△BMD是等腰直角三角形.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x+4的图象与反比例函数y2=![]() 的图象交于A(﹣1,a),B两点,与x轴交于点C.
的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求k.
(2)根据图象直接写出y1>y2时,x的取值范围.
(3)若反比例函数y2=![]() 与一次函数y1=x+4的图象总有交点,求k的取值.
与一次函数y1=x+4的图象总有交点,求k的取值.

查看答案和解析>>
科目:初中数学 来源: 题型:
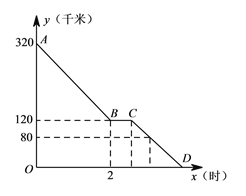
【题目】上周六上午![]() 点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离
点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离![]() (千米)与他们路途所用的时间
(千米)与他们路途所用的时间![]() (时)之间的函数图象,请根据以上信息,解答下列问题:
(时)之间的函数图象,请根据以上信息,解答下列问题:
(1)求直线![]() 所对应的函数关系式;
所对应的函数关系式;
(2)已知小颖一家出服务区后,行驶![]() 分钟时,距姥姥家还有
分钟时,距姥姥家还有![]() 千米,问小颖一家当天几点到达姥姥家?
千米,问小颖一家当天几点到达姥姥家?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB-BC→CD向点D运动设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所小示,则AD的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织一次“研学之旅”活动,现用抽签的方式从以下四个地方:九峰公园、柑橘博览园、平田桐树坑、长潭水库(其中九峰公园、平田桐树坑是爱国主义教育基地)中确定两个作为活动地点.将四个地点分别写在4张完全相同的卡片上,背面朝上并洗匀,先从中随机抽取一张卡片,再从剩下的卡片中随机抽取一张.则“抽中的两个地方都是爱国主义教育基地”的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C、D为监测点,已知点C、D、B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°
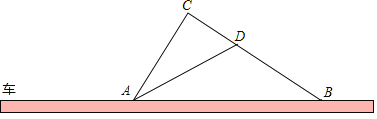
(1)求道路AB段的长(结果精确到1米)
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由;参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年5月5日,中国邮政发行《马克思诞辰200周年》纪念邮票1套2枚(如图),这套邮票正面图案为:马克思像、马克思与恩格斯像,背面完全相同.发行当日,小宇购买了此款纪念邮票2套,他将2套邮票沿中间虚线撕开(使4枚形状、大小完全相同)后将4枚纪念邮票背面朝上放在桌面上,并随机从中抽出2张,则抽出的2张邮票恰好都是“马克思像”的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用两个月时间试销某种新型商品,经市场调查,该商品的第![]() 天的进价
天的进价![]() (元/件)与
(元/件)与![]() (天)之间的相关信息如下表:
(天)之间的相关信息如下表:
时间 |
|
|
进价 |
| 40 |
该商品在销售过程中,销售量![]() (件)与
(件)与![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
在销售过程中,商场每天销售的该产品以每件80元的价格全部售出.
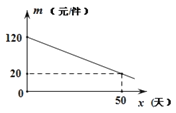
(1)求该商品的销售量![]() (件)与
(件)与![]() (天)之间的函数关系;
(天)之间的函数关系;
(2)设第![]() 天该商场销售该商品获得的利润为
天该商场销售该商品获得的利润为![]() 元,求出
元,求出![]() 与
与![]() 之间的函数关系式,并求出第几天销售利润最大,最大利润是多少元?
之间的函数关系式,并求出第几天销售利润最大,最大利润是多少元?
(3)在销售过程中,当天的销售利润不低于2400元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com