
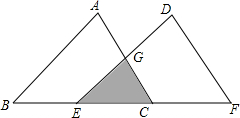
 如图,将△ABC沿AB方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的$\frac{1}{3}$.已知BC=3,求△ABC平移的距离.
如图,将△ABC沿AB方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的$\frac{1}{3}$.已知BC=3,求△ABC平移的距离. 分析 移动的距离可以视为FC或BE的长度,根据题意可知△ABC与阴影部分为相似三角形,且面积比为3:1,所以BC:EC=$\sqrt{3}$:1,推出EC=$\sqrt{3}$,所以BE=3-$\sqrt{3}$,从而求解.
解答 解:∵△ABC沿AB边平移到△DEF的位置,
∴AC∥DF,
∴△ABC∽△DBG,
∴$\frac{{S}_{阴影面积}}{{S}_{△ABC}}=(\frac{EC}{BC})^{2}=\frac{1}{3}$,
∴BC:EC=$\sqrt{3}$:1,
∵BC=3,
∴EC=$\sqrt{3}$,
∴△ABC平移的距离为3-$\sqrt{3}$.
点评 本题主要考查相似三角形的判定和性质、平移的性质,关键在于求证△ABC与阴影部分为相似三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 要对一棵倾斜的古杉树AB进行保护,BC是暂时用来支撑的支架.需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,求支架BC的长度.(结果取整数)
要对一棵倾斜的古杉树AB进行保护,BC是暂时用来支撑的支架.需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,求支架BC的长度.(结果取整数)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
测试项目 | 测试成绩 | ||
| A | B | C | |
| 笔 试 | 90 | 80 | 75 |
| 面 试 | 85 | 85 | 85 |
| 群众评议 | 77 | 84 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
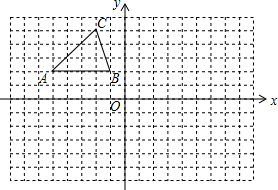 在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(-1,2).
在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com