
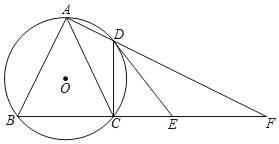
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,AD、BC的延长线交于点F,点E在CF上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)当AB=AC时,若CE=2,EF=3,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先判断出BD是圆O的直径,再判断出BD⊥DE,即可得出结论;
(2)根据余角的性质和等腰三角形的性质得到∠F=∠EDF,根据等腰三角形的判定得到DE=EF=3,根据勾股定理得到CD![]() ,证明△CDE∽△DBE,根据相似三角形的性质即可得到结论.
,证明△CDE∽△DBE,根据相似三角形的性质即可得到结论.
(1)如图,连接BD.
∵∠BAD=90°,∴点O必在BD上,即:BD是直径,∴∠BCD=90°,∴∠DEC+∠CDE=90°.
∵∠DEC=∠BAC,∴∠BAC+∠CDE=90°.
∵∠BAC=∠BDC,∴∠BDC+∠CDE=90°,∴∠BDE=90°,即:BD⊥DE.
∵点D在⊙O上,∴DE是⊙O的切线;
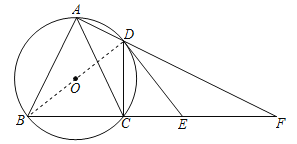
(2)∵∠BAF=∠BDE=90°,∴∠F+∠ABC=∠FDE+∠ADB=90°.
∵AB=AC,∴∠ABC=∠ACB.
∵∠ADB=∠ACB,∴∠F=∠FDE,∴DE=EF=3.
∵CE=2,∠BCD=90°,∴∠DCE=90°,∴CD![]() .
.
∵∠BDE=90°,CD⊥BE,∴∠DCE=∠BDE=90°.
∵∠DEC=∠BED,∴△CDE∽△DBE,∴![]() ,∴BD
,∴BD![]() ,∴⊙O的半径
,∴⊙O的半径![]() .
.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴正半轴相交于A、B两点,与
轴正半轴相交于A、B两点,与![]() 轴相交于点C,对称轴为直线
轴相交于点C,对称轴为直线![]() 且OA=OC,则下列结论:①
且OA=OC,则下列结论:①![]() ②
②![]() ③
③![]() ④关于
④关于![]() 的方程
的方程![]() 有一个根为
有一个根为![]() 其中正确的结论个数有( )
其中正确的结论个数有( )
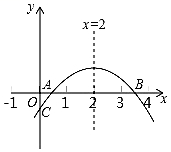
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自驾游是当今社会一种重要的旅游方式,五一放假期间小明一家人自驾去灵山游玩,下图描述了小明爸爸驾驶的汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )
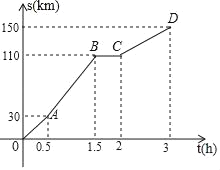
A. 汽车在0~1小时的速度是60千米/时; B. 汽车在2~3小时的速度比0~0.5小时的速度快;
C. 汽车从0.5小时到1.5小时的速度是80千米/时; D. 汽车行驶的平均速度为60千米/时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙O的圆心A的坐标为(1,0),半径为1,点P为直线y=![]() x+3上的动点,过点P作⊙A的切线,且点为B,则PB的最小值是 .
x+3上的动点,过点P作⊙A的切线,且点为B,则PB的最小值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
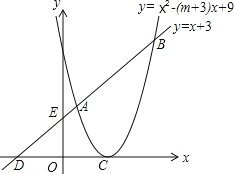
【题目】如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.
(1)求m的值;
(2)求A、B两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
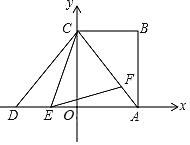
【题目】如图,矩形ABCD的顶点A、C在平面直角坐标系的坐标轴上,AB=4,CB=3,点D与点A关于y轴对称,点E、F分别是线段DA、AC上的动点(点E不与A、D重合),且∠CEF=∠ACB,若△EFC为等腰三角形,则点E的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
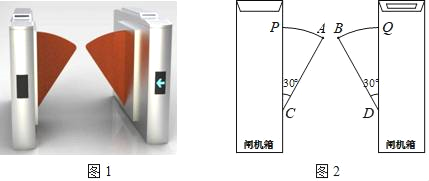
A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com