
分析 (1)先把各二次根式化为最简二次根式,再把括号内合并后进行二次根式的乘法运算,然后合并即可;
(2)先变形得到原式=[$\sqrt{2}$+($\sqrt{3}$-$\sqrt{6}$)]•[$\sqrt{2}$-($\sqrt{3}$-$\sqrt{6}$)],然后利用平方差公式和完全平方公式计算.
解答 解:(1)原式=4$\sqrt{2}$-(2$\sqrt{3}$-$\sqrt{3}$)×$\sqrt{6}$
=4$\sqrt{2}$-$\sqrt{3}$×$\sqrt{6}$
=4$\sqrt{2}$-3$\sqrt{2}$
=$\sqrt{2}$;
(2)原式=[$\sqrt{2}$+($\sqrt{3}$-$\sqrt{6}$)]•[$\sqrt{2}$-($\sqrt{3}$-$\sqrt{6}$)]
=($\sqrt{2}$)2-($\sqrt{3}$-$\sqrt{6}$)2
=2-(3-6$\sqrt{2}$+6)
=2-9+6$\sqrt{2}$
=-7+6$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:解答题
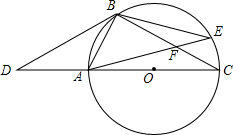 如图,点D是⊙O的直径CA延长线上的一点,点B在⊙O上,且AB=AD=AO.
如图,点D是⊙O的直径CA延长线上的一点,点B在⊙O上,且AB=AD=AO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
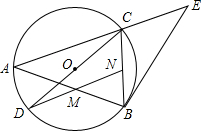 如图,△ABE中,过A、B两点的⊙O交AE于点C,CD为直径,过点D作DN∥AC分别交AB、BC于M、N,AB=AC,∠ABE=90°+∠ACD.
如图,△ABE中,过A、B两点的⊙O交AE于点C,CD为直径,过点D作DN∥AC分别交AB、BC于M、N,AB=AC,∠ABE=90°+∠ACD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
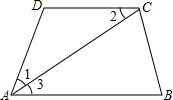 如图,AC平分∠DAB,∠1=∠2,试说明AB∥CD.
如图,AC平分∠DAB,∠1=∠2,试说明AB∥CD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2<x<6 | B. | 3<x<9 | C. | 1<x<9 | D. | 2<x<8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com