
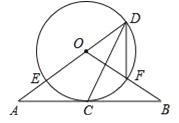
【题目】如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.
(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长.
【答案】(1)①证明见解析;②证明见解析;(2)![]() .
.
【解析】
试题分析:(1)①欲证明直线AB是⊙O的切线,只要证明OC⊥AB即可.
②首先证明OC∥DF,再证明∠FDC=∠OCD,∠EDC=∠OCD即可.
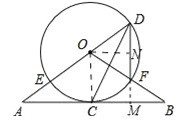
(2)作ON⊥DF于N,延长DF交AB于M,在RT△CDM中,求出DM、CM即可解决问题.
试题解析:(1)①证明:连接OC.
∵OA=OB,AC=CB,∴OC⊥AB,∵点C在⊙O上,∴AB是⊙O切线.
②证明:∵OA=OB,AC=CB,∴∠AOC=∠BOC,∵OD=OF,∴∠ODF=∠OFD,∵∠AOB=∠ODF+∠OFD=∠AOC+∠BOC,∴∠BOC=∠OFD,∴OC∥DF,∴∠CDF=∠OCD,∵OD=OC,∴∠ODC=∠OCD,∴∠ADC=∠CDF.
(2)作ON⊥DF于N,延长DF交AB于M.
∵ON⊥DF,∴DN=NF=3,在RT△ODN中,∵∠OND=90°,OD=5,DN=3,∴ON=![]() =4,∵∠OCM+∠CMN=180°,∠OCM=90°,∴∠OCM=∠CMN=∠MNO=90°,∴四边形OCMN是矩形,∴ON=CM=4,MN=OC=5,在RT△CDM中,∵∠DMC=90°,CM=4,DM=DN+MN=8,∴CD=
=4,∵∠OCM+∠CMN=180°,∠OCM=90°,∴∠OCM=∠CMN=∠MNO=90°,∴四边形OCMN是矩形,∴ON=CM=4,MN=OC=5,在RT△CDM中,∵∠DMC=90°,CM=4,DM=DN+MN=8,∴CD=![]() =
=![]() =
=![]() .
.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次食品安检中,抽查某企业10袋奶粉,每袋取出100克,检测每100克奶粉蛋白质含量与规定每100克含量(蛋白质)比较,不足为负,超过为正,记录如下:(注:规定每100g奶粉蛋白质含量为15g)-3,-4,-5,+1,+3,+2,0,-1.5,+1,+2.5
(1)求平均每100克奶粉含蛋白质为多少?
(2)每100克奶粉含蛋白质不少于14克为合格,求合格率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F. 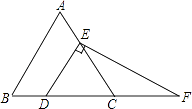
(1)求∠F的度数;
(2)若CD=2,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.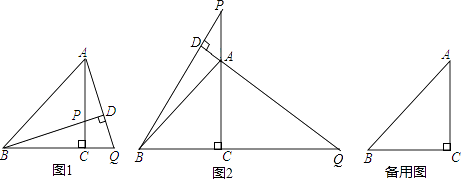
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立?(填“成立”或“不成立”)
(3)在(2)的条件下,当∠DBA=度时,存在AQ=2BD,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.
(1)k的值是 ;
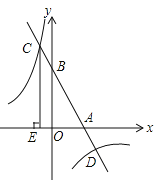
(2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数![]() 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若
图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若![]() ,则b的值是 .
,则b的值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com