
【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.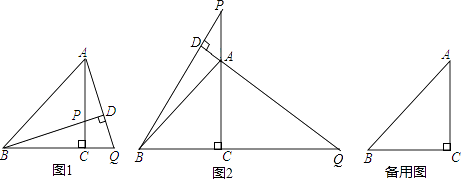
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立?(填“成立”或“不成立”)
(3)在(2)的条件下,当∠DBA=度时,存在AQ=2BD,说明理由.
【答案】
(1)
证明:∵∠ACB=∠ADB=90°,∠APD=∠BPC,
∴∠DAP=∠CBP,
在△ACQ和△BCP中 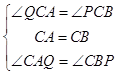
∴△ACQ≌△BCP(ASA),
∴BP=AQ
(2)成立
(3)22.5°
【解析】(2.)成立,
理由:延长BA交PQ于H,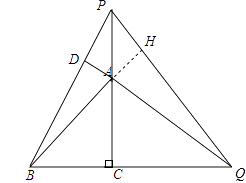
∵∠ACQ=∠BDQ=90°,∠AQC=∠BQD,
∴∠CAQ=∠DBQ,
在△AQC和△BPC中, 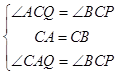
∴△AQC≌△BPC(ASA),
∴AQ=BP,
所以答案是:成立;
(3.)当∠DBA=22.5°时,存在AQ=2BD,
理由:∵∠BAC=∠DBA+∠APB=45°,
∴∠PBA=∠APB=22.5°,
∴AP=AB,
∵AD⊥BP,
∴BP=2BD,
在△PBC与△QAC中, 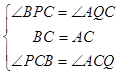 ,
,
∴△PBC≌△ACQ,
∴AQ=PB,
∴AQ=2BD.
所以答案是:22.5°


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
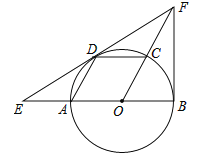
【题目】如图,AB是⊙O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.
(1)求证:BF是⊙O的切线;
(2)已知圆的半径为1,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A(﹣3,﹣5)向右平移2个单位,再向下平移3个单位到点B,则点B的坐标为( )
A.(﹣5,﹣8)
B.(﹣5,﹣2)
C.(﹣1,﹣8)
D.(﹣1,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
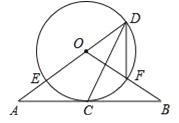
【题目】如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.
(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
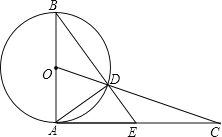
【题目】如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD.
(1)求证:△CDE∽△CAD;
(2)若AB=2,AC=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() (a>0,a为常数)和
(a>0,a为常数)和![]() 在第一象限内的图象如图所示,点M在
在第一象限内的图象如图所示,点M在![]() 的图象上,MC⊥x轴于点C,交
的图象上,MC⊥x轴于点C,交![]() 的图象于点A;MD⊥y轴于点D,交
的图象于点A;MD⊥y轴于点D,交![]() 的图象于点B,当点M在
的图象于点B,当点M在![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①S△ODB=S△OCA;
②四边形OAMB的面积不变;
③当点A是MC的中点时,则点B是MD的中点.
其中正确结论的个数是( )
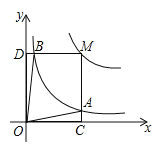
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.
求∠FDC和∠AHB的度数.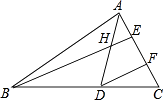
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com