
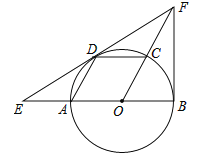
【题目】如图,AB是⊙O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.
(1)求证:BF是⊙O的切线;
(2)已知圆的半径为1,求EF的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)先证明四边形AOCD是菱形,从而得到∠AOD=∠COD=60°,再根据切线的性质得∠FDO=90°,接着证明△FDO≌△FBO得到∠ODF=∠OBF=90°,然后根据切线的判定定理即可得到结论;
(2)在Rt△OBF中,利用60度的正切的定义求解.
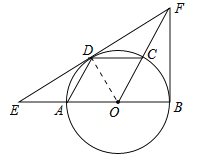
试题解析:(1)证明:连结OD,如图,∵四边形AOCD是平行四边形,而OA=OC,∴四边形AOCD是菱形,∴△OAD和△OCD都是等边三角形,∴∠AOD=∠COD=60°,∴∠FOB=60°,∵EF为切线,∴OD⊥EF,∴∠FDO=90°,在△FDO和△FBO中,∵OD=OB,∠FOD=∠FOB,FO=FO,∴△FDO≌△FBO,∴∠ODF=∠OBF=90°,∴OB⊥BF,∴BF是⊙O的切线;
(2)解:在Rt△OBF中,∵∠FOB=60°,而tan∠FOB=![]() ,∴BF=1×tan60°=
,∴BF=1×tan60°=![]() .∵∠E=30°,∴EF=2BF=
.∵∠E=30°,∴EF=2BF=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,在数轴上A点表示数a,B点表示数b,a、b满足|a+2|+|b-6|=0。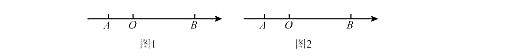
(1)点A表示的数为,点B表示的数为;
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=BC,则C点表示的数为;
(3)如图2,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左动。在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒)。
①分别表示出甲、乙两小球到原点的距离(用t表示)
②求甲、乙两小球到原点的距离相等时经历的时间。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校篮球队五名主力队员的身高分别是174,179,180,174,178(单位:cm),则这五名队员身高的中位数是( )
A.174cm B.177cm C.178cm D.180cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元
(1)设租用甲种货车x辆(x为非负整数),试填写表格.
表一:

表二:

(2)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.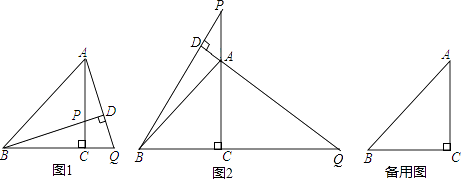
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立?(填“成立”或“不成立”)
(3)在(2)的条件下,当∠DBA=度时,存在AQ=2BD,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com