
【题目】公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元
(1)设租用甲种货车x辆(x为非负整数),试填写表格.
表一:

表二:

(2)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.
【答案】(1)表一:315,45x,30,﹣30x+240;表二:1200,400x,1400,﹣280x+2240;(2)甲种货车6辆,乙种货车2辆.
【解析】
试题分析:(1)由题意可得,在表一中,当甲车7辆时,运送的机器数量为:45×7=315(台),则乙车8﹣7=1辆,运送的机器数量为:30×1=30(台),当甲车x辆时,运送的机器数量为:45×x=45x(台),则乙车(8﹣x)辆,运送的机器数量为:30×(8﹣x)=﹣30x+240(台),在表二中,当租用甲货车3辆时,租用甲种货车的费用为:400×3=1200(元),则租用乙种货车8﹣3=5辆,租用乙种货车的费用为:280×5=1400(元),当租用甲货车x辆时,租用甲种货车的费用为:400×x=400x(元),则租用乙种货车(8﹣x)辆,租用乙种货车的费用为:280×(8﹣x)=﹣280x+2240(元),故答案为:表一:315,45x,30,﹣30x+240;
表二:1200,400x,1400,﹣280x+2240;
(2)能完成此项运送任务的最节省费用的租车方案是甲车6辆,乙车2辆,理由:当租用甲种货车x辆时,设两种货车的总费用为y元,则两种货车的总费用为:y=400x+(﹣280x+2240)=120x+2240,又∵45x+(﹣30x+240)≥330,解得x≥6,∵120>0,∴在函数y=120x+2240中,y随x的增大而增大,∴当x=6时,y取得最小值,即能完成此项运送任务的最节省费用的租车方案是甲种货车6辆,乙种货车2辆.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】已知线段AB=30cm.
(1)如图1,点P沿线段AB自点A向点B以2cm/s的速度运动,同时点Q沿线段BA自点B向点A以3cm/s的速度运动,几秒钟后,P、Q两点相遇?
(2)几秒后,点P、Q两点相距10cm?
(3)如图2,AO=PO=4cm,∠POB=60°,现点P绕着点O以30°/秒的速度逆时针旋转一周停止,同时点Q沿直线自B点向A点运动,假若点P、Q两点能相遇,求点Q的运动速度.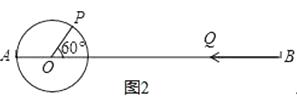
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为100米的正三角形花坛的边上,甲、乙两人分别从两个顶点同时出发,按逆时针方向行走,已知甲的速度是42米/分,乙的速度是34米/分.出发后分钟,甲乙两人第一次走在同一条边上. 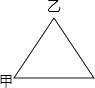
查看答案和解析>>
科目:初中数学 来源: 题型:
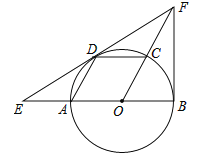
【题目】如图,AB是⊙O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.
(1)求证:BF是⊙O的切线;
(2)已知圆的半径为1,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,后求值;
(1)(5x﹣3y﹣2xy)﹣(6x+5y﹣2xy),其中x=﹣5,y=1
(2)(a2b﹣2ab)﹣(3ab2+4ab),其中a=2,b=﹣ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王鹏家里购买了一套小户型商品房,准备将地面铺上相同的地砖,地面结构如下图,根据图中的数据(单位:m),解答下列问题. 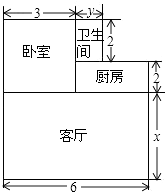
(1)用含x,y的代数式表示地面总面积;
(2)已知铺1m2地砖的平均费用为210元,当x=5,y=1时,求铺这套商品房所需地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
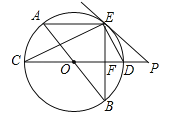
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A(﹣3,﹣5)向右平移2个单位,再向下平移3个单位到点B,则点B的坐标为( )
A.(﹣5,﹣8)
B.(﹣5,﹣2)
C.(﹣1,﹣8)
D.(﹣1,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
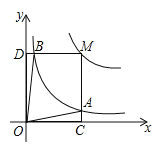
【题目】反比例函数![]() (a>0,a为常数)和
(a>0,a为常数)和![]() 在第一象限内的图象如图所示,点M在
在第一象限内的图象如图所示,点M在![]() 的图象上,MC⊥x轴于点C,交
的图象上,MC⊥x轴于点C,交![]() 的图象于点A;MD⊥y轴于点D,交
的图象于点A;MD⊥y轴于点D,交![]() 的图象于点B,当点M在
的图象于点B,当点M在![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①S△ODB=S△OCA;
②四边形OAMB的面积不变;
③当点A是MC的中点时,则点B是MD的中点.
其中正确结论的个数是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com