
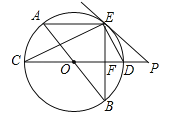
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
【答案】(1)证明见试题解析;(2)证明见试题解析;(3)![]() .
.
【解析】
试题分析:(1)如图,连接OE,证明OE⊥PE即可得出PE是⊙O的切线;
(2)由圆周角定理得到∠AEB=∠CED=90°,进而得到∠3=∠4,结合已知条件证得结论;
(3)设EF=x,则CF=2x,在RT△OEF中,根据勾股定理求出EF的长,进而求得BE,CF的长,在RT△AEB中,根据勾股定理求出AE的长,然后根据△AEB∽△EFP,求出PF的长,即可求得PD的长.
试题解析:(1)如图,连接OE.∵CD是圆O的直径,∴∠CED=90°,∵OC=OE,∴∠1=∠2,又∵∠PED=∠C,即∠PED=∠1,∴∠PED=∠2,∴∠PED+∠OED=∠2+∠OED=90°,即∠OEP=90°,∴OE⊥EP,又∵点E在圆上,∴PE是⊙O的切线;
(2)∵AB、CD为⊙O的直径,∴∠AEB=∠CED=90°,∴∠3=∠4(同角的余角相等),又∵∠PED=∠1,∴∠PED=∠4,即ED平分∠BEP;
(3)设EF=x,则CF=2x,∵⊙O的半径为5,∴OF=2x﹣5,在RT△OEF中,![]() ,即
,即![]() ,解得x=4,∴EF=4,∴BE=2EF=8,CF=2EF=8,∴DF=CD﹣CF=10﹣8=2,∵AB为⊙O的直径,∴∠AEB=90°,∵AB=10,BE=8,∴AE=6,∵∠BEP=∠A,∠EFP=∠AEB=90°,∴△AEB∽△EFP,∴
,解得x=4,∴EF=4,∴BE=2EF=8,CF=2EF=8,∴DF=CD﹣CF=10﹣8=2,∵AB为⊙O的直径,∴∠AEB=90°,∵AB=10,BE=8,∴AE=6,∵∠BEP=∠A,∠EFP=∠AEB=90°,∴△AEB∽△EFP,∴![]() ,即
,即![]() ,∴PF=
,∴PF=![]() ,∴PD=PF﹣DF=
,∴PD=PF﹣DF=![]() =
=![]() .
.



 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】某校篮球队五名主力队员的身高分别是174,179,180,174,178(单位:cm),则这五名队员身高的中位数是( )
A.174cm B.177cm C.178cm D.180cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元
(1)设租用甲种货车x辆(x为非负整数),试填写表格.
表一:

表二:

(2)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,点A的坐标为(﹣4,3),点B的坐标为(﹣3,1),BC=2,BC∥x轴. 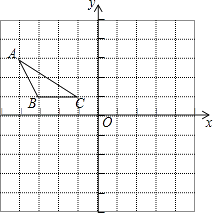
(1)画出△ABC关于y轴对称的图形△A1B1C1;并写出A1 , B1 , C1的坐标;
(2)求以点A、B、B1、A1为顶点的四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据2016年南平市政府工作报告,2015年全市外贸出口11.26亿美元,这一数据用科学记数法表示为( )
A. 0.1126×1010 B. 1.126×109
C. 1.126×108 D. 11.26×107
查看答案和解析>>
科目:初中数学 来源: 题型:
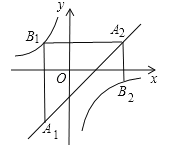
【题目】如图,已知点A1,A2,…,An均在直线![]() 上,点B1,B2,…,Bn均在双曲线
上,点B1,B2,…,Bn均在双曲线![]() 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若![]() ,则a2015= .
,则a2015= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com