
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F. 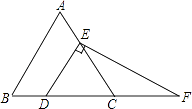
(1)求∠F的度数;
(2)若CD=2,求DF的长.
科目:初中数学 来源: 题型:
【题目】为加强公民的节水意识,合理利用水资源.某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于1:1.5:2.如图折线表示实行阶梯水价后每月水费y(元)与用水量xm3之间的函数关系.其中线段AB表示第二级阶梯时y与x之间的函数关系.
(1)写出点B的实际意义;
(2)求线段AB所在直线的表达式;
(3)某户5月份按照阶梯水价应缴水费102元,其相应用水量为多少立方米?

查看答案和解析>>
科目:初中数学 来源: 题型:
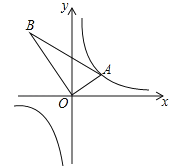
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数![]() 的图象上.若点B在反比例函数
的图象上.若点B在反比例函数![]() 的图象上,则k的值为( )
的图象上,则k的值为( )
A.﹣4 B.4 C.﹣2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
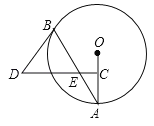
【题目】如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若CD=15,BE=10,tanA=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
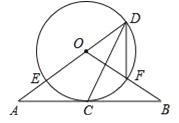
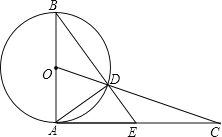
【题目】如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.
(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD.
(1)求证:△CDE∽△CAD;
(2)若AB=2,AC=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块直角三角形绿地,量得两直角边长分别为3m,4m,现在要将绿地扩充成等腰三角形,且扩充时只能延长两条直角边中的一条,则扩充后等腰三角形绿地的面积为m2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
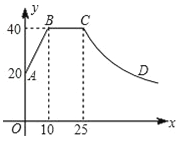
【题目】一般情况下,学生注意力上课后逐渐增强,中间有段时间处于较理想的稳定状态,随后开始分散.实验结果表明,学生注意力指数y随时间x(min)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)上课后第5min与第30min相比较,何时学生注意力更集中?
(2)某道难题需连续讲19min,为保证效果,学生注意力指数不宜低于36,老师能否在所需要求下讲完这道题?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com