
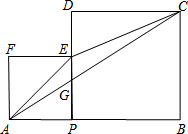
 如图,AB=a,P是线段AB上任意一点(点P不与A、B重合),分别以AP,BP为边作正方形APEF、正方形PBCD,点E在边PD上.设AP=x.
如图,AB=a,P是线段AB上任意一点(点P不与A、B重合),分别以AP,BP为边作正方形APEF、正方形PBCD,点E在边PD上.设AP=x.分析 (1)分别求得正方形APEF、正方形PBCD的面积相加即可;
(2))利用△AEC的面积=两个正方形的面积之和S-△ABC的面积-△AEF的面积-△ECD的面积求得答案,并利用所求面积找得答案即可.
解答 解(1)因为AP=x,AB=a,则BP=a-x,
所以S=x2+(a-x)2
=2x2-2ax+a2;
(2)△AEC的面积=两个正方形的面积之和S-△ABC的面积-△AEF的面积-△ECD的面积=$\frac{1}{2}$x2,
∵△APG的面积=$\frac{1}{2}$x2-△AEG的面积,△CEG的面积=$\frac{1}{2}$x2-△AEG的面积,
∴△APG的面积=△CEG的面积.
点评 此题考查整式的混合运算,掌握面积之间的关系是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | y=2(x-3) | B. | y=2x-3 | C. | y=2x+3 | D. | y=2x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)(a-b)=a2-b2 | B. | a2+2ab+b2=(a+b)2 | C. | a(a+b)=a2+ab | D. | (a-b)2=(b-a)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
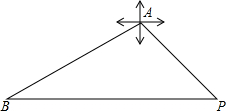 北京时间2014年3月8日凌晨1时20分,由马来西亚飞往北京的马来西亚航空公司MH370航班于地面失去联系,机上239人中包括153名中国大陆乘客.飞机可能出事的海域在点P的正西方向且距离P约2000海里的点B处,中国海上搜救中心的海警船3411在点A观测P点在东偏南45度方向,观测飞机疑似“终结”区域点B在点A的西偏南30度方向,海警船点A到疑似出事区域点B的距离.
北京时间2014年3月8日凌晨1时20分,由马来西亚飞往北京的马来西亚航空公司MH370航班于地面失去联系,机上239人中包括153名中国大陆乘客.飞机可能出事的海域在点P的正西方向且距离P约2000海里的点B处,中国海上搜救中心的海警船3411在点A观测P点在东偏南45度方向,观测飞机疑似“终结”区域点B在点A的西偏南30度方向,海警船点A到疑似出事区域点B的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com