
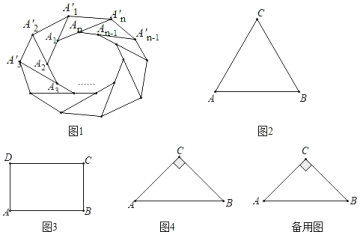
【题目】定义:按螺旋式分别延长n边形的n条边至一点,若顺次连接这些点所得的图形与原多边形相似,则称它为原图形的螺旋相似图形.例如:如图1,分别延长多边形A1A2…An的边得A1′,A2′,…,An′,若多边形A1′A2′…An′与多边形A1A2…An相似,则多边形A1′A2′…An′就是A1A2…An的螺旋相似图形.
(1)如图2,已知△ABC是等边三角形,作出△ABC的一个螺旋相似图形,简述作法,并给以证明.
(2)如图3,已知矩形ABCD,请探索矩形ABCD是否存在螺旋相似图形,若存在,求出此时AB与BC的比值;若不存在,说明理由.
(3)如图4,△ABC是等腰直角三角形,AC=BC=2,分别延长CA,AB,BC至A′,B′,C′,使△A′B′C′是△ABC的螺旋相似三角形.若AA′=kAC,请直接写出BB′,CC′的长(用含k的代数式表示)
【答案】(1)见解析;(2)AB:BC=1;(3)BB′=![]() k,CC′=k.
k,CC′=k.
【解析】
(1)如图2中,延长AB到E,延长BC到F,延长CA到D,使得BE=CF=AD,连接EF,DF,DE.则△DEF是△ABC的一个螺旋相似图形,证明△DEF是等边三角形即可解决问题.
(2)如图3中,假设存在.四边形EFGH是矩形ABCD的螺旋相似图形,设AB=CD=a,BC=AD=b,BE=DG=x,CF=AH=y.分两种情形,利用相似三角形的性质以及相似矩形的性质,构建关系式证明a=b即可解决问题.
(3)如图4中,作B′T⊥CB交CB的延长线于T.设TB=TB′=m,证明△A′CC′≌△A′TB′(ASA),推出A′C=TC′,CC′=TB′=BT,构建关系式推出m=k即可解决问题.
解:(1)如图2中,延长AB到E,延长BC到F,延长CA到D,使得BE=CF=AD,连接EF,DF,DE.则△DEF是△ABC的一个螺旋相似图形.
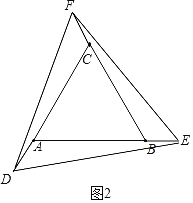
理由:∵△ABC是等边三角形,
∴AB=BC=AC,∠CAB=∠ABC=∠ACB,
∴∠DAE=∠FCD=∠EBF=120°,
∵BE=CF=AD,
∴CD=AE=BF,
∴△FCD≌△DAE≌△EBF(SAS),
∴DF=DE=EF,
∴△DEF是等边三角形,
∴△DEF∽△ABC,
∴△DEF是△ABC的一个螺旋相似图形.
(2)如图3中,假设存在.四边形EFGH是矩形ABCD的螺旋相似图形,设AB=CD=a,BC=AD=b,BE=DG=x,CF=AH=y.
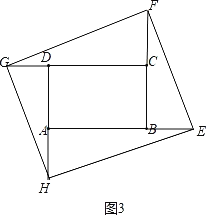
由题意:△BEF∽△AHE,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
当![]() =
=![]() =
=![]() 时,
时,![]() =
=![]() =
=![]() ,
,
∴x=![]() y,ax+x2=by+y2,
y,ax+x2=by+y2,
∴by+![]() y2=by+y2,
y2=by+y2,
∴a2=b2,
∴a=b,即AB:BC=1.
当![]() =
=![]() =
=![]() 时.
时.![]() =
=![]() =
=![]() ,
,
∴x=![]() y,ax+x2=by+y2,
y,ax+x2=by+y2,
∴![]() y+
y+![]() y2=by+y2,
y2=by+y2,
∴![]() y(1+
y(1+![]() )=0,
)=0,
∵y≠0,1+![]() ≠0,
≠0,
∴a2=b2,
∴a=b,即AB:BC=1,
综上所述,AB:BC=1.
(3)如图4中,作B′T⊥CB交CB的延长线于T.
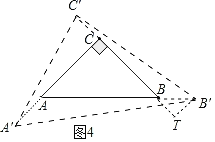
∵AC=BC=2,∠ACB=90°,
∴∠ABC=∠CAB=45°,
∴∠TBB′=∠ABC=45°,
∴∠TB′B=∠TBB′=45°,
∴TB=TB′,设TB=TB′=m,
∵△A′B′C′是△ABC的螺旋相似三角形,
∴A′C′=B′C′,∠A′C′B′/span>=90°,
∵∠A′C′C+∠B′C′=90°,∠A′CC+∠C′A′C=90°,
∴∠C′A′C=∠B′C′T,
∵∠A′CC′=∠T=90°,
∴△A′CC′≌△A′TB′(ASA),
∴A′C=TC′,CC′=TB′=BT,
∴2+2k=2+2m,
∴m=k,
∴BB′=![]() k,CC′=k.
k,CC′=k.


科目:初中数学 来源: 题型:
【题目】二次函数y=x2+bx+c的图象经过坐标原点O和点A(7,0),直线AB交y轴于点B(0,﹣7),动点C(x,y)在直线AB上,且1<x<7,过点C作x轴的垂线交抛物线于点D,则CD的最值情况是( )
A.有最小值9B.有最大值9C.有最小值8D.有最大值8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC所在平面上的动点,连接OB,OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.

(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,点O所在位置应满足什么条件?(直接写出答案不需要说明理由.)
(3)在图2中作出点O,使得四边形DGFE是正方形(保留作图痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+m与二次函数y=ax2+2x+c的图象交于点A(0,3),已知该二次函数图象的对称轴为直线x=1.
(1)求m的值及二次函数解析式;
(2)若直线y=x+m与二次函数y=ax2+2x+c的图象的另一个交点为B,求△OAB的面积;
(3)根据函数图象回答:x为何值时该一次函数值大于二次函数值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点A,B在x轴的负半轴上,反比例函数y=![]() (k1≠0)在第二象限内的图象经过正方形ABCD的顶点D(m,2)和BC边上的点G(n,
(k1≠0)在第二象限内的图象经过正方形ABCD的顶点D(m,2)和BC边上的点G(n,![]() ),直线y=k2x+b(k2≠0)经过点D,点G,则不等式
),直线y=k2x+b(k2≠0)经过点D,点G,则不等式![]() ≤k2x+b的解集为__________.
≤k2x+b的解集为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2014兰州)兰州市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表(如图①)和频数分布直方图(如图②)的一部分.
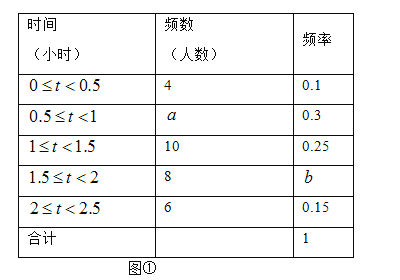
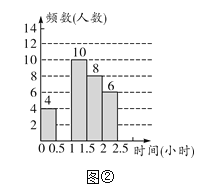
(1)在图①中,![]() ________,
________,![]() ________;
________;
(2)补全频数分布直方图;
(3)请估计该校1400名初中学生中,约有多少学生在1.5小时以内完成了家庭作业.
查看答案和解析>>
科目:初中数学 来源: 题型:
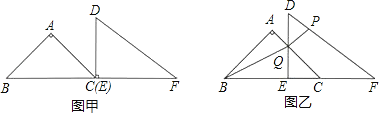
【题目】已知:把Rt△ABC和Rt△DEF按如图甲摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠BAC=∠DEF=90°,∠ABC=45°,BC=9cm,DE=6cm,EF=8cm.如图乙,△DEF从图甲的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△DEF的顶点F出发,以3cm/s的速度沿FD向点D匀速移动.当点P移动到点D时,P点停止移动,△DEF也随之停止移动.DE与AC相交于点Q,连接BQ、PQ,设移动时间为t(s).解答下列问题:
(1)设三角形BQE的面积为y(cm2),求y与t之间的函数关系式,并写出自变量t的取值范围;
(2)当t为何值时,三角形DPQ为等腰三角形?
(3)是否存在某一时刻t,使P、Q、B三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
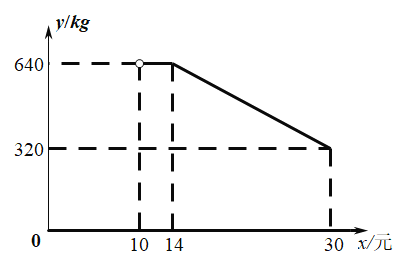
【题目】![]() 年春节期间,新型冠状病毒肆虐,突如其来的疫情让大多数人不能外出,网络销售成为这个时期最重要的一种销售方式。某乡镇贸易公司因此开设了一家网店,销售当地某种农产品。已知该农产品成本为每千克
年春节期间,新型冠状病毒肆虐,突如其来的疫情让大多数人不能外出,网络销售成为这个时期最重要的一种销售方式。某乡镇贸易公司因此开设了一家网店,销售当地某种农产品。已知该农产品成本为每千克![]() 元,调查发现,每天销售量
元,调查发现,每天销售量![]() 与销售单价
与销售单价![]() (元)满足如图所示的函数关系(其中
(元)满足如图所示的函数关系(其中![]() )
)
(1)求![]() 与
与![]() 之间的函数关系式并标出自变最
之间的函数关系式并标出自变最![]() 的取值范围;
的取值范围;
(2)当销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com