
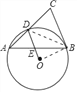
【题目】如图,△ABC中,∠A=45°,D是AC边上一点,⊙O经过D、A、B三点,OD∥BC.
(1)求证:BC与⊙O相切;
(2)若OD=15,AE=7,求BE的长.
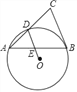
【答案】(1)见解析;(2)18.
【解析】分析:(1)连接OB,求出∠DOB度数,根据平行线性质求出∠CBO=90°,根据切线判定得出即可;
(2)延长BO交⊙O于点F,连接AF,求出∠ABF,解直角三角形求出BE.
详解:(1)证明:连接OB.
∵∠A=45°,
∴∠DOB=90°.
∵OD∥BC,
∴∠DOB+∠CBO=180°.
∴∠CBO=90°.
∴直线BC是⊙O的切线.
(2)解:连接BD.则△ODB是等腰直角三角形,
∴∠ODB=45°,BD=![]() OD=15
OD=15![]() ,
,
∵∠ODB=∠A,∠DBE=∠DBA,
∴△DBE∽△ABD,
∴BD2=BEBA,
∴(15![]() )2=(7+BE)BE,
)2=(7+BE)BE,
∴BE=18或﹣25(舍弃),
∴BE=18.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
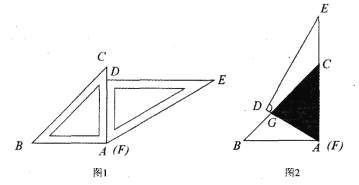
【题目】一副三角板按图 1 所示的位置摆放,将△DEF 绕点 A(F)逆时针旋转 60°后(图 2), 测得 CG=8cm,则两个三角形重叠(阴影)部分的面积为()
A. 16+16 ![]() cm2
cm2
B. 16+![]() cm2
cm2
C. 16+![]() cm2
cm2
D. 48cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A顺时针旋转60°得到△ADE,点C的对应点E恰好落在BA的延长线上,DE与BC交于点F,连接BD.下列结论不一定正确的是( )
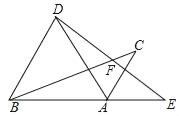
A. AD=BD B. AC∥BD C. DF=EF D. ∠CBD=∠E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),与x轴的另一个交点在点(1,0)和(2,0)之间,对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③a+c>0;④2a+c<0,其中正确的结论个数是( )
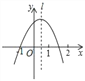
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级为奖励参加校运动会的运动员,分别用160元和120元购买了相同数量的甲、乙两种奖品,其中每件甲种奖品比每件乙种奖品贵4元.
请你根据以上信息,提出一个用分式方程解决的问题,并写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() cm,
cm,![]() cm,在
cm,在![]() 中,
中,![]() ,
,![]() cm,
cm,![]() cm.EF在BC上,保持
cm.EF在BC上,保持![]() 不动,并将
不动,并将![]() 以1cm/s的速度向点C运动,移动开始前点F与点B重合,当点E与点C重合时,
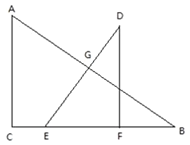
以1cm/s的速度向点C运动,移动开始前点F与点B重合,当点E与点C重合时,![]() 停止移动.边DE与AB相交于点G,连接FG,设移动时间为t(s).
停止移动.边DE与AB相交于点G,连接FG,设移动时间为t(s).
(1)![]() 从移动开始到停止,所用时间为________s;
从移动开始到停止,所用时间为________s;
(2)当DE平分AB时,求t的值;
(3)当![]() 为等腰三角形时,求t的值.
为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
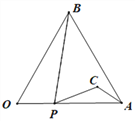
【题目】如图,等边△AOB的边长为4,点P从点O出发,沿OA以每秒1个单位的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA.在点P从O向A运动的过程中,当△PCA为直角三角形时t的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
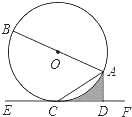
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
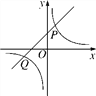
【题目】如图,直线y=k1x+1与双曲线y=![]() 相交于P(1,m),Q(-2,-1)两点.
相交于P(1,m),Q(-2,-1)两点.
(1)求m的值;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上三点,且x1<x2<0<x3,请直接说明y1,y2,y3的大小关系;
(3)观察图象,请直接写出不等式k1x+1>![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com