
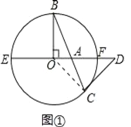
����Ŀ��ͬѧ�Ƕ�ѧϰ�������Ρ��α��������199ҳ�ĵ�11�⣬���������ģ���ͼ��AΪ��O��ֱ��EF�ϵ�һ�㣬OB�Ǻ�����ֱ����ֱ�İ뾶��BA�͡�O�ཻ����һ��C������C�����ߺ�EF���ӳ����ཻ�ڵ�D����֤��DA��DC��

��1���ֽ�ͼ1�е�ֱ��EF����ֱ�߽���ƽ���ƶ���ͼ2��ʾ��λ�ã���ʱOB��EF��ֱ�ཻ��H�������������䣮
����֤��DA��DC��
�ڵ�DF��EF��1��8����DF��![]() ʱ����ABAC��ֵ��
ʱ����ABAC��ֵ��
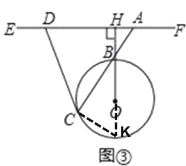
��2����ͼ2�е�EF����ֱ��������ƽ���ƶ���ͼ3��ʾ��λ�ã�ʹEF��OB���ӳ��ߴ�ֱ�ཻ��H��AΪEF������H��һ�㣬��AHС�ڡ�O�����߽�EF��D���Բ��룺DA��DC�Ƿ���Ȼ������֤����Ľ��ۣ�
���𰸡���1���ټ�������24��2������DA��DC��Ȼ����
��������
��1��������OC���������ߵ�������ɵõ�OC��DC��Ȼ��õ���DCA=90��-��ACO=90��-��B=��DAC�����õȽǶԵȱߵõ�DA=DC���ɣ�
������DF��EF=1��8��DF=![]() ��ɵõ�EF=8DF=8
��ɵõ�EF=8DF=8![]() ��Ȼ���������߳��������DC�ij��������õ�DC��AD�ij���Ȼ���������߳������ã�ABAC=AEAF=24��
��Ȼ���������߳��������DC�ij��������õ�DC��AD�ij���Ȼ���������߳������ã�ABAC=AEAF=24��
��2��������Ȼ�������ӳ�BO����O��K����CK���������ߵ����ʿ��Եõ���DCA=��CKB=90��-��CBK���Ӷ��õ���DCA=��BAH�������֤.
��1����֤������OC����OC��DC��
���DCA��90�㩁��ACO��90�㩁��B��
�֡�DAC����BAE��90�㩁��B��
���DAC����DCA��DA��DC��
�ڡ�DF��EF��1��8��DF��![]() ��
��
��EF��8DF��8![]() ��
��
��DCΪ���ߣ�
��DC2��DFDE��![]() ��9
��9![]() ��18��
��18��
��DC��3![]() ��
��
��AD��DC��3![]() ��
��
��AF��AD��DF��2![]() ��
��
��AE��EF��AF��6![]() ��
��
��ABAC��AEAF��24��
��2������DA��DC��Ȼ�������������£�
�ӳ�BO����O��K����CK�����KCB��90�㣬
��DCΪ��O�����ߣ�
���DCA����CKB��90�㩁��CBK��
�֡�BAH��90�㩁��HBA��
����CBK����HBA��
���DCA����BAH��
��DA��DC��


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ƽ��ֱ������ϵ�У�ͼ��G�ϵ�P��x��y����������y���������x�IJ�y��x��ΪP����������������ͼ��G�����е������������е����ֵ��Ϊͼ��G��������ֵ����
��1���ٵ�A��1��3�������������Ϊ�� ����
��������y����x2+3x+4��������ֵ��Ϊ�� ����
��2��ij���κ���y����x2+bx+c��c��0����������ֵ��Ϊ��1����B��m��0�����C�ֱ��Ǵ˶��κ�����ͼ����x���y��Ľ��㣬�ҵ�B���C�������������ȣ�
��ֱ��д��m���� �������ú�c��ʽ�ӱ�ʾ��
����˶��κ����ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c(a��0)��y�ύ�ڵ�C����x�ύ��A��B���㣬���е�B������ΪB(4��0)�������ߵĶԳ��ύx���ڵ�D��CE��AB�����������ߵĶԳ��ύ�ڵ�E�������н��ۣ���b2��4a��0����b��0����5a+b��0����AD+CE��4��������ȷ���۸���Ϊ( )
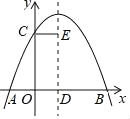
A. 4 B. 3 C. 2 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���������40�����ʵ��������һ�����꾭Ӫ���˽һ�ֳɱ�Ϊ20Ԫ/����������Ʒ�ڵ�x�����۵������Ϣ���±���ʾ��
������p������ | P=50��x |
| ��1��x��20ʱ�� |
��1�������ڼ������Ʒ�����۵���Ϊ35Ԫ/����
��2����������x���õ�����y����x�ĺ�����ϵʽ��
��3����40���и�����ڼ����õ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
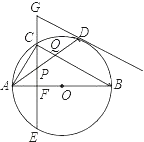
����Ŀ����ͼ���ڡ�O�У�AB��ֱ������D�ǡ�O��һ�㣬��C��![]() ���е㣬��CE��AB�ڵ�F������D�����߽�EC���ӳ����ڵ�G������AD���ֱ�CF��BC�ڵ�P��Q������AC���������н��ۣ��١�BAD����ABC����GP��GD���۵�P�ǡ�ACQ�����ģ���APAD��CQCB��������ȷ����_____��д��������ȷ���۵���ţ���
���е㣬��CE��AB�ڵ�F������D�����߽�EC���ӳ����ڵ�G������AD���ֱ�CF��BC�ڵ�P��Q������AC���������н��ۣ��١�BAD����ABC����GP��GD���۵�P�ǡ�ACQ�����ģ���APAD��CQCB��������ȷ����_____��д��������ȷ���۵���ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������y��mx2+��m��2��x��2m+2��m��0����
��1����֤����������x���н��㣻
��2������������x�ύ�ڵ�A��x1��0����B��x2��0������A�ڵ�B���Ҳ࣬��x1+2x2��1��
����m��ֵ��
����P���������ϣ���G��n����![]() n��
n��![]() ������PG����Сֵ��
������PG����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijͬѧ��һ����ҵ��Ľ���˼·��������ʦ���ݴ�չ�������ۣ�������ͼ����֪A��1��![]() ����B��4��0������OAB��ƽ����AC��x���ڵ�C����OC�ij���˼·����AD��OB��CE��AB��CF��OA
����B��4��0������OAB��ƽ����AC��x���ڵ�C����OC�ij���˼·����AD��OB��CE��AB��CF��OA
��A�����OD��1��AD��![]() ��OA��2����AOC��60�㣻
��OA��2����AOC��60�㣻
��A��B�����OA��2��OB��4��AB��2![]() ����OAB��90�㣻
����OAB��90�㣻
��ACƽ�֡�OAB��CE��CF��
��S��AOC+S��ABC��S��AOB��AOCF+ABCE��OAAB��CF��3��![]() ��
��
�����ϣ�Rt��OCF�У�OC��![]() ��2�������Ż���
��2�������Ż���
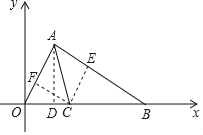
��1��ͬѧ�Ƿ��ֲ���Ҫ֤����OAB��90�㡱Ҳ����⣬��Ҫ˵�����ɣ���λͬѧ����˲�ͬ��˼·
�ټ�˵��S��AOC��S��ABC�����֮�ȼ���![]() ������
������![]() ���Ӷ�
���Ӷ�![]() ��
��
����˵����AB����ȡ��G��ʹAG��AO������CG����֪BG�ij���Ϊ����
�۱�˵���ӳ�AC����AOB�����Բ��N��������һ�κ������������OC��
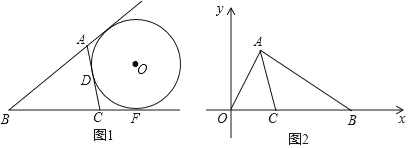
����ѡ������һ�ֽⷨ������ͼ2�����в�����ɽ����ʲô�ջ�
��2���������ͼ��������ȷ��������ϵ����Ч�������������������⣺��ͼ1����O���ABC�ı�AC����BA��BC���ӳ���AE��CF���У��е�ֱ�ΪD��E��F�����ABC�����ΪS��BC��a��AC��b��AB��c�����ú�S��a��b��c��ʽ�ӱ�ʾ��O�İ뾶R��ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������x�Ķ��κ���![]() ��ͼ����x�ύ�ڵ�A(1��0)�͵�B����y�ύ�ڵ�C(0��3)�������ߵĶԳ�����x�ύ�ڵ�D.
��ͼ����x�ύ�ڵ�A(1��0)�͵�B����y�ύ�ڵ�C(0��3)�������ߵĶԳ�����x�ύ�ڵ�D.
(1)����κ����ı���ʽ��
(2)��y�����Ƿ����һ��P��ʹ��PBCΪ����������.�����ڣ��������P�����ꣻ
(3)��һ����M�ӵ�A��������ÿ��1����λ���ٶ���AB�����B�˶�����һ����N�ӵ�D���Mͬʱ��������ÿ��2����λ���ٶ��������ߵĶԳ������˶�������M�� ���Bʱ����M��Nͬʱֹͣ�˶����ʵ�M��N�˶����δ�ʱ����MNB�����������������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B=90������O�ڱ�AB�ϣ��Ե�OΪԲ�ģ�OAΪ�뾶��Բ������C������C��ֱ��MN��ʹ��BCM=2��A��
��1���ж�ֱ��MN����O��λ�ù�ϵ����˵�����ɣ�
��2����OA=4����BCM=60������ͼ����Ӱ���ֵ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com