
【题目】定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y﹣x称为P点的“坐标差”,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”.
(1)①点A(1,3)的“坐标差”为 ;
②抛物线y=﹣x2+3x+4的“特征值”为 ;
(2)某二次函数y=﹣x2+bx+c(c≠0)的“特征值”为﹣1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等.
①直接写出m= ;(用含c的式子表示)
②求此二次函数的表达式.
【答案】(1)①2;②5;(2)①m=-c;②y=﹣x2+3x-2
【解析】
(1)①由题中所给“坐标差”的定义即可得到点A(1,3)的坐标差.
②由坐标差的定义可得:二次函数y=-x2+3x+4图象上点的坐标差为:y-x=-x2+3x+3-x=-x2+2x+3,将此关系式配方即可求得y-x的最大值,从而得到抛物线y=-x2+3x+4的“特征值”.
(2)①由题意可得:0-m=c-0,由此可得:m=-c.
②由m=-c可得点B的坐标为(-c,0),把点B的坐标代入y=x2+bx+c(c≠0)中可得c(c-b+1)=0,由c≠0可得c-b+1=0,即b=c+1.再由y=x2+bx+c(c≠0)的特征值为-1可得:![]() =-1,两者即可解得b和c的值,由此即可得到二次函数的解析式.
=-1,两者即可解得b和c的值,由此即可得到二次函数的解析式.
(1)①2.②4.
点A(1,3)的“坐标差”为3-1=2,抛物线y=﹣x2+3x+4的“特征值”为-x2+3x+4-x的最大值,-x2+3x+4-x=-x2+2x+4=-(x2-2x+1-1)+4=-(x-1)2+5,所以抛物线y=﹣x2+3x+4的“特征值”为5.
(2)①m=-c.
②∵m=-c
∴B(-c,0)
将其代入 y=-x2+bx+c中,
得-c2-bc+c=0
∵c≠0
∴-c-b+1=0
∴b=-c+1①
∴其“坐标差”为:y-x=-x2+bx+c-x=-x2+(b-1)x+c.
∵“特征值”为-1.
∴![]() =-1 ②.
=-1 ②.
将①代入②中,得c=-2.
∴b=-c+1=3.
∴抛物线的表达式为y=-x2+3x-2.


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC.
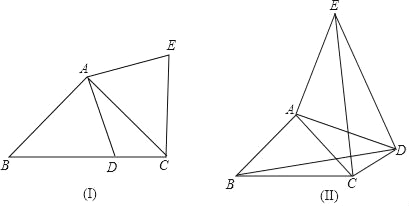
(I)如图,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC.
求证:(1)△BAD≌△CAE;
(2)BC=DC+EC.
(Ⅱ)如图,D为△ABC外一点,且∠ADC=45°,仍将线段AD绕点A逆时针旋转90°得到AE,连接EC,ED.
(1)△BAD≌△CAE的结论是否仍然成立?并请你说明理由;
(2)若BD=9,CD=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)为了掌握我市中考模拟数学试题的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为160分)分为5组:第一组85~10;第二组100~115;第三组115~130;第四组130~145;第五组145~160,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列问题:
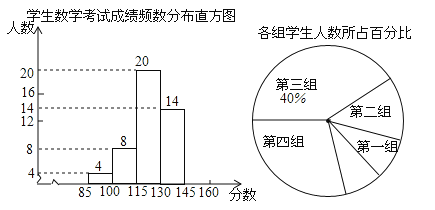
(1)本次调查共随机抽取了该年级多少名学生?并将频数分布直方图补充完整;
(2)若将得分转化为等级,规定:得分低于100分评为“D”,100~130分评为“C”,130~145分评为“B”,145~160分评为“A”,那么该年级1500名考生中,考试成绩评为“B”的学生大约有多少名?
(3)如果第一组只有一名是女生,第五组只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想,请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种品牌羽绒服和防寒服,其中羽绒服的售价是防寒服售价的5倍还多100元,2014年1月份(春节前期)共销售500件,羽绒服与防寒服销量之比是4:1,销售总收入为58.6万元.
(1)求羽绒服和防寒服的售价;
(2)春节后销售进入淡季,2014年2月份羽绒服销量下滑了6m%,售价下滑了4m%,防寒服销量和售价都维持不变,结果销售总收入下降为16.04万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1,A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1,A3B2∥A2B1,A3B3∥A2B2,A4B3∥A3B2,…. 若![]() 和
和![]() 的面积分别为1、9,则
的面积分别为1、9,则![]() 的面积是_________.
的面积是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
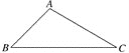
【题目】三角形中有3个角、3条边共6个元素,由其中的已知元素,求出所有未知元素的过程,叫做解三角形.
已知△ABC中,AB=![]() ,∠B=45°,BC=1+
,∠B=45°,BC=1+![]() ,解△ABC.
,解△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都学习过《几何》课本第三册第199页的第11题,它是这样的:如图,A为⊙O的直径EF上的一点,OB是和这条直径垂直的半径,BA和⊙O相交于另一点C,过点C的切线和EF的延长线相交于点D,求证:DA=DC.

(1)现将图1中的直径EF所在直线进行平行移动到图2所示的位置,此时OB与EF垂直相交于H,其它条件不变.
①求证:DA=DC;
②当DF:EF=1:8,且DF=![]() 时,求ABAC的值.
时,求ABAC的值.
(2)将图2中的EF所在直线继续向上平行移动到图3所示的位置,使EF与OB的延长线垂直相交于H,A为EF上异于H的一点,且AH小于⊙O的切线交EF于D,试猜想:DA=DC是否仍然成立?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com