
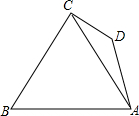
 四边形ABCD中,BC⊥CD,∠BCA=60°,∠CDA=135°,BC=10.S△ABC=20$\sqrt{3}$.求AD边的长.
四边形ABCD中,BC⊥CD,∠BCA=60°,∠CDA=135°,BC=10.S△ABC=20$\sqrt{3}$.求AD边的长. 分析 作AF⊥AC于F,作AE⊥CD交CD的延长线于E,利用三角形的面积公式S△ABC=$\frac{1}{2}$BC•AF和锐角三角函数的概念求解.
解答 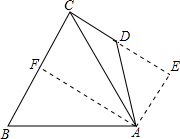 解:作AF⊥BC于F,作AE⊥CD交CD的延长线于E.
解:作AF⊥BC于F,作AE⊥CD交CD的延长线于E.
∵S△ABC=$\frac{1}{2}$BC•AF=$\frac{1}{2}$×10×AF=20$\sqrt{3}$,
∴AF=4$\sqrt{3}$,
∵sin∠BCA=sin60°=AF:AC=$\frac{\sqrt{3}}{2}$,
∴AC=8.
∵BC⊥CD,AE⊥CD
∴∠CAE=∠BCA=60°,
∴∠ACD=90°-60°=30°,
∵∠CDA=135°,
∴AE=ED=sin∠ACD•AC=4.
在等腰直角三角形中AD=$\sqrt{2}$AE=4$\sqrt{2}$.
点评 本题考查了解直角三角形,等腰直角三角形的性质,三角形的面积公式,正确的作出辅助线是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 1.2×107 | B. | 1.2×108 | C. | 12×107 | D. | 12×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
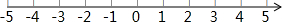 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 捐款金额(元) | 5 | 10 | 15 | 20 | 50 |
| 捐款人数(人) | a | 18 | 10 | 12 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对称轴都是x轴 | B. | 最低点都是原点(0,0) | ||
| C. | 在y轴右侧呈下降趋势 | D. | 形状相同,开口方向相反 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com