
| 第1行 | 1 2 3 |
| 第2行 | 4 5 6 7 8 |
| 第3行 | 9 10 11 12 13 14 15 |
| 第4行 | 16 17 18 19 20 21 22 23 24 |
| … | … |
分析 首先根据第1行的数的个数是3=2×1+1,第2行的数的个数是5=2×2+1,第3行的数的个数是7=2×3+1,第4行的数的个数是9=2×4+1,…,可得第n行的数的个数是2n+1,然后应用等差数列的求和公式,求出前n行的数的总个数是多少,即可判断出第n行从右向左数的第5个数是多少.
解答 解:∵第1行的数的个数是3=2×1+1,
第2行的数的个数是5=2×2+1,
第3行的数的个数是7=2×3+1,
第4行的数的个数是9=2×4+1,
…,
∴第n行的数的个数是2n+1,
∴前n行的数的总个数是:
[3+(2n+1)]×n÷2
=(2n+4)×n÷2
=n2+2n
∴第n行从右向左数的第5个数是n2+2n-4.
故答案为:n2+2n-4.
点评 此题主要考查了探寻数列规律问题,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结出规律,并能正确的应用规律,解答此题的关键是判断出:第n行的数的个数是2n+1,并能应用等差数列的求和公式,求出前n行的数的总个数是多少.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
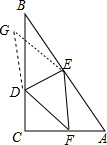 如图,已知Rt△ABC的两条直角边,AC=6,BC=8,点D是BC边上的点,过D作DE⊥AB于E,点F是AC边上的动点,连结DF,EF,以DF、EF为邻边构造?DFEG:
如图,已知Rt△ABC的两条直角边,AC=6,BC=8,点D是BC边上的点,过D作DE⊥AB于E,点F是AC边上的动点,连结DF,EF,以DF、EF为邻边构造?DFEG:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
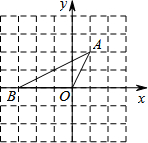 如图,把直角坐标系xOy放置在边长为1的正方形网格中,O是坐标原点,点A、O、B均在格点上,将△OAB绕O点按顺时针方向旋转90°后,得到△OA′B′.
如图,把直角坐标系xOy放置在边长为1的正方形网格中,O是坐标原点,点A、O、B均在格点上,将△OAB绕O点按顺时针方向旋转90°后,得到△OA′B′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
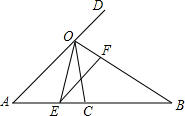 如图,∠AOB的平分线OC与线段AB交于点C,点D在AO的延长线上,作射线OE使得OB平分∠DOE,OE交AB于点E.
如图,∠AOB的平分线OC与线段AB交于点C,点D在AO的延长线上,作射线OE使得OB平分∠DOE,OE交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
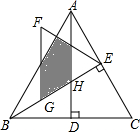 如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{5\sqrt{3}}{2}$.
如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{5\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B.
如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com