
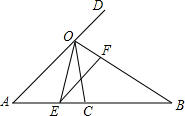
 如图,∠AOB的平分线OC与线段AB交于点C,点D在AO的延长线上,作射线OE使得OB平分∠DOE,OE交AB于点E.
如图,∠AOB的平分线OC与线段AB交于点C,点D在AO的延长线上,作射线OE使得OB平分∠DOE,OE交AB于点E.分析 (1)根据同位角相等,两直线平行即可得到结论;
(2)由角平分线的性质和平角的定义可得结论;
(3)根据角平分线的性质和平角的定义即可得到结论.
解答 解:(1)EF∥AD,
理由; ∵∠DOB=∠EOB,∠DOB+∠AOB=180°,
∵∠DOB=∠EOB,∠DOB+∠AOB=180°,
∵∠EOF+∠EFB=180°,
∴∠AOB=∠EFB,
∴EF∥AD;
(2)∵OB平分∠DOE,
∴∠DOB=∠BOE,
∵OC平分∠AOB,
∴∠AOC=∠BOC,
∵OE平分∠AOC,
∴∠AOE=∠COE,
设∠AOE=∠COE=α,则∠BOC=2α,∠DOB=∠BOE=3α,
∴α+3α+3α=180°,
∴α=$\frac{180}{7}$,
∴∠AOC=2α=($\frac{360}{7}$)°
(3)当点E落在点A上,∵∠DOB=∠BOD,
∴∠DOB=∠BOA=90°,
∵∠AOC=$\frac{1}{2}$∠BOA=45°,
当点E落在点C上时,
∠AOC=∠BOC=∠BOD=$\frac{1}{3}$×180°=60°,
∴若点E只能落在线段AC上(不含点A,C)时,∠AOC的取值范围是45°<∠AOC<60°.
点评 本题考查了平行线的判定和性质,角平分线的性质,熟练掌握角平分线的性质定理是解题的关键.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:选择题
| A. | 将抛物线C向右平移$\frac{5}{2}$个单位 | B. | 将抛物线C向右平移3个单位 | ||
| C. | 将抛物线C向右平移5个单位 | D. | 将抛物线C向右平移6个单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 第1行 | 1 2 3 |
| 第2行 | 4 5 6 7 8 |
| 第3行 | 9 10 11 12 13 14 15 |
| 第4行 | 16 17 18 19 20 21 22 23 24 |
| … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
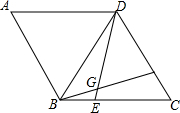 在菱形ABCD中,AB=BD,点E,F分别在BC,CD上,且BE=CF,连接BF,DE交于点G.若BG=3,DG=4,则四边形ABGD的面积为$\frac{49}{4}\sqrt{3}$.
在菱形ABCD中,AB=BD,点E,F分别在BC,CD上,且BE=CF,连接BF,DE交于点G.若BG=3,DG=4,则四边形ABGD的面积为$\frac{49}{4}\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
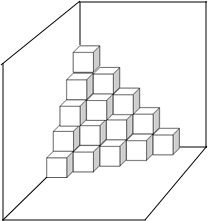 如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层.
如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
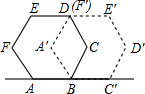 如图,将正六边形ABCDEF绕点B顺时针旋转后到达A′BC′D′E′F′的位置,所转过的度数是( )
如图,将正六边形ABCDEF绕点B顺时针旋转后到达A′BC′D′E′F′的位置,所转过的度数是( )| A. | 60° | B. | 72° | C. | 108° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com