
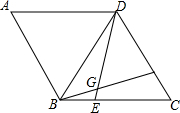
 在菱形ABCD中,AB=BD,点E,F分别在BC,CD上,且BE=CF,连接BF,DE交于点G.若BG=3,DG=4,则四边形ABGD的面积为$\frac{49}{4}\sqrt{3}$.
在菱形ABCD中,AB=BD,点E,F分别在BC,CD上,且BE=CF,连接BF,DE交于点G.若BG=3,DG=4,则四边形ABGD的面积为$\frac{49}{4}\sqrt{3}$. 分析 首先利用菱形的性质得出AB=AD,又由AB=BD得出△ABD是等边三角形,进一步证明△CDE≌△DBF,得出∠BGE=∠DGF=60°,证得四边形ABGD是圆内接四边形,过点A再分别作AM⊥DE,AN⊥BF,证明△ABN≌△ADM,把四边形ABGD的面积转化为四边形AMGN的面积即可.
解答 解:∵四边形ABCD是菱形,
∴AB=AD,
又∵AB=BD,
∴△ABD是等边三角形,
∴∠BAD=∠ABD=60°
∴∠DBC=∠BDF=∠C=60°
∵BE=CF,
∴CE=DF,
在△CDE和△DBF中,
$\left\{\begin{array}{l}{CD=DB}\\{∠C=∠BDF}\\{CE=DF}\end{array}\right.$,
∴△CDE≌△DBF(SAS),
∴∠CDE=∠DBF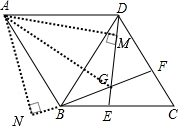 ,
,
∴∠GBE=∠BDE,
∴∠DBF+∠GBE=∠DBF+∠BDE=∠BGE=∠DGF=60°=∠BAD,
∴四边形ABGD是圆内接四边形,
∵AD=AB,
∴∠AGB=∠AGD=60°,
如图,过点A分别作AM⊥DE,AN⊥BF,垂足分别为M、N,
∵AG是角平分线,
∴AN=AM,
在Rt△ABN和Rt△ADM中,
$\left\{\begin{array}{l}{AN=AM}\\{AB=AD}\end{array}\right.$
∴Rt△ABN≌Rt△ADM(HL),
∴BN=DM,
∴GN+GM=BG+DG=3+4=7,
在Rt△AGN和Rt△AGM中
$\left\{\begin{array}{l}{AN=AM}\\{AG=AG}\end{array}\right.$,
∴Rt△AGN≌Rt△AGM(HL),
∴NG=MG=$\frac{1}{2}$(BG+DG)=$\frac{7}{2}$,
∴AN=NG•tan∠AGN=$\frac{7\sqrt{3}}{2}$,
∵S四边形ABGD=S四边形ANGM.
∴S四边形ABGD=2S△AGN=2×$\frac{1}{2}$×NG×AN=$\frac{7}{2}$×$\frac{7\sqrt{3}}{2}$=$\frac{49\sqrt{3}}{4}$.
故答案为:$\frac{49\sqrt{3}}{4}$.
点评 此题考查菱形的性质,等边三角形的判定,三角形全等的判定与性质,圆内接四边形的判定与性质等知识点,发现四边形ABGD是圆内接四边形是解决问题的关键.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:选择题
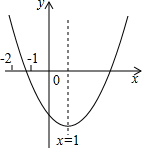 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
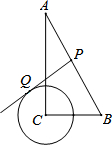 如图,在Rt△ABC中,∠C=Rt∠,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为( )
如图,在Rt△ABC中,∠C=Rt∠,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2-$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
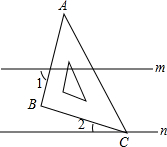 如图,直线m∥n,将含有45°角的三角板ABC的一个锐角顶点C放在直线n上,则∠1+∠2等于( )
如图,直线m∥n,将含有45°角的三角板ABC的一个锐角顶点C放在直线n上,则∠1+∠2等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
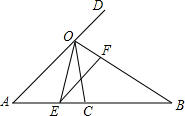 如图,∠AOB的平分线OC与线段AB交于点C,点D在AO的延长线上,作射线OE使得OB平分∠DOE,OE交AB于点E.
如图,∠AOB的平分线OC与线段AB交于点C,点D在AO的延长线上,作射线OE使得OB平分∠DOE,OE交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $y=\frac{1}{2}{x^2}$ | B. | y=x2+2x | C. | y=x2+x+2 | D. | y=x2-x-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
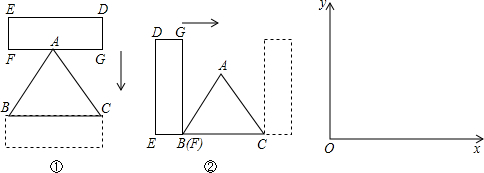
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com