
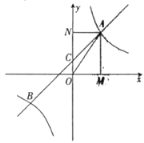
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第一、三象限内的
的图象交于第一、三象限内的![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,过点
点,过点![]() 作
作![]() 轴于点
轴于点![]() ,作
,作![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求四边形![]() 的周长和面积.
的周长和面积.
(2)求该反比例函数和一次函数的解析式.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
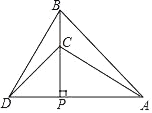
【题目】如图,△PAB与△PCD均为等腰直角三角形,点C在PB上,若△ABC与△BCD的面积之和为10,则△PAB与△PCD的面积之差为( )
A. 5B. 10C. l5D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
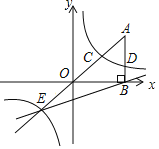
【题目】如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,cos∠OAB═![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为
的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为![]() .
.
(1)求反比例函数的解析式;
(2)求直线EB的解析式;
(3)求S△OEB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队需完成A、B两个工地的工程.若甲、乙两个工程队分别可提供40个和50个标准工作量,完成A、B两个工地的工程分别需要70个和20个标准工作量,且两个工程队在A、B两个工地的1个标准工作量的成本如下表所示:
A工地 | B工地 | |
甲工程队 | 800元 | 750元 |
乙工程队 | 600元 | 570元 |
设甲工程队在A工地投入x(20≤x≤40)个标准工作量,完成这两个工程共需成本y元.
(1)求y与x之间的函数关系式;
(2)请判断y是否能等于62000,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解全区3000名九年级学生英语听力口语自动化考试成绩的情况,随机抽取了部分学生的成绩(满分30分且得分均为整数),制成下表:
分数段(x分分) | 0≤x≤18 | 19≤x≤21 | 22≤x≤24 | 25≤x≤27 | 28≤x≤30 |
人数 | 10 | 15 | 35 | 112 | 128 |
(1)填空:
①本次抽样调查共抽取了 名学生;
②学生成绩的中位数所在的分数段是 ;
③若用扇形统计图表示统计结果,则分数段为0≤x≤18的人数所对应扇形的圆心角为 °;
(2)如果将25分以上(含25分)定为优秀,请估计全区九年级考生成绩为优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,数轴上有A、B两点.
(1)线段AB的中点表示的数是 ;
(2)线段AB的长度是 ;
(3)若A、B两点问时向右运动,A点速度是每秒3个单位长度,B点速度是每秒2个单位长度,问经过几秒时AB=2?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.
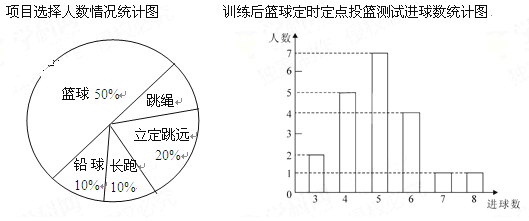
请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为 度,该班共有学生 人, 训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
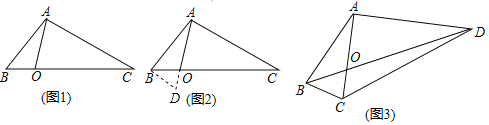
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=![]() ,BO:CO=1:3,求AB的长.
,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com