
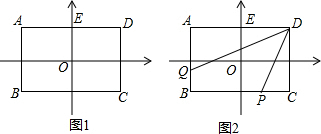
分析 (1)利用矩形的性质和对称性,由点D的坐标直接得出答案即可;
(2)得出E点的坐标为(0,3),设出M点的坐标,根据△CME的面积是长方形ABCD面积的$\frac{1}{6}$,列出方程解答即可;
(3)由B点的横坐标为6-2t=-6,得出t=6,求得点P的运动速度为2,点Q的运动速度为1,利用面积差表示出四边形PBQD的面积比较得出答案即可.
解答 解:(1)A、B、C的坐标分别为(-6,3)、(-6,-3)、(6,-3);
(2)由题意得E点的坐标为(0,3),设M点坐标为(0,a),
则$\frac{1}{2}$×|a-3|×6=$\frac{1}{6}$×12×6
解得:a=-1或a=7,
M点坐标为(0,-1)或(0,7).
(3)∵B点的横坐标为6-2t=-6,
∴t=6,
则点P的运动速度为12÷6=2,点Q的运动速度为2÷2=1,
①CP=2t,AQ=6-t;
②不变.
理由:∵四边形PBQD的面积=12×6-$\frac{1}{2}$(6-t)×12-$\frac{1}{2}$×2t×6=36,
∴四边形PBQD的面积不发生变化.
点评 此题考查坐标与图形的性质,三角形的面积,矩形的性质与面积,掌握矩形的对称性是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
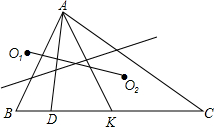 设D是△ABC的边BC上一点,但不是中点,设O1和O2分别是△ABD和△ADC的外心,求证:△ABC的中线AK的垂直平分线过线段O1O2中点.
设D是△ABC的边BC上一点,但不是中点,设O1和O2分别是△ABD和△ADC的外心,求证:△ABC的中线AK的垂直平分线过线段O1O2中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B,延长BO与⊙O交于点D,与PA的延长线交于点E,
如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B,延长BO与⊙O交于点D,与PA的延长线交于点E,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com