17.
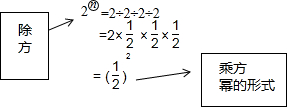
概念学习
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2,(-3)÷(-3)÷(-3)÷(-3)等. 类比有理数的乘方,我们把2÷2÷2记作2
③,读作“2的圈2次方”,(-3)÷(-3)÷(-3)÷(-3)记作(-3)
④,读作“-3的圈4次方”,一般地,把$\underbrace{a÷a÷a÷…÷a}_{n个a}$(a≠0)记作a
?,读作“a的圈n次方”.
初步探究
(1)直接写出计算结果:2
③=$\frac{1}{2}$,$(-\frac{1}{2})$
⑤=-$\frac{1}{8}$;
(2)关于除方,下列说法错误的是C
A.任何非零数的圈2次方都等于1; B.对于任何正整数n,1
?=1;
C.3
④=4
③ D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
深入思考
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
(1)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.(-3)
④=$\frac{1}{{3}^{2}}$;5
⑥=$\frac{1}{{5}^{4}}$;<“m“:math xmlns:dsi='http://www.dessci.com/uri/2003/MathML'dsi:zoomscale='150'dsi:_mathzoomed='1'style='CURSOR:pointer; DISPLAY:inline-block'>(-12)$(-\frac{1}{2})$
⑩=$\frac{1}{{2}^{8}}$.
(2)想一想:将一个非零有理数a的圈n次方写成幂的形式等于$\frac{1}{{a}^{n-2}}$;
(3)算一算:${12^2}÷{(-\frac{1}{3})^④}×{(-\frac{1}{2})^⑤}-{(-\frac{1}{3})^⑥}÷{3^3}$.

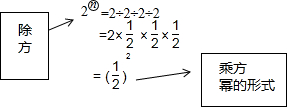 概念学习
概念学习