
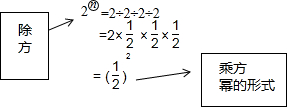 概念学习
概念学习分析 初步探究
(1)根据新定义计算;
(2)根据新定义可判断C错误;
深入思考
(1)把有理数的除方运算转化为乘方运算进行计算;
(2)利用新定义求解;
(3)先把除方运算转化为乘方运算进行计算,然后进行乘除运算.
解答 解:初步探究
(1)2③=$\frac{1}{2}$,$(-\frac{1}{2})$⑤=-$\frac{1}{8}$;
(2)C选项错误;
深入思考
(1)(-3)④=$\frac{1}{{3}^{2}}$;5⑥=$\frac{1}{{5}^{4}}$;$(-\frac{1}{2})$⑩=$\frac{1}{{2}^{8}}$.
(2)a?=$\frac{1}{{a}^{n-2}}$;
(3)原式=122÷32×(-23)-34÷33
=-131.
故答案为$\frac{1}{2}$,-$\frac{1}{8}$,C,$\frac{1}{{3}^{2}}$,$\frac{1}{{5}^{4}}$,$\frac{1}{{2}^{8}}$,$\frac{1}{{a}^{n-2}}$.
点评 本题考查了有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.


科目:初中数学 来源: 题型:解答题
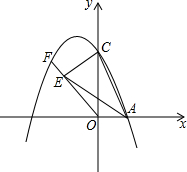 已知抛物线y=-x2+2x+3与x轴正半轴交于A点,与y轴正半轴交于点C,点F在抛物线上,且在第二象限,CE⊥OF于点E,连AC、AE.若AE=AC,求直线OF的解析式.
已知抛物线y=-x2+2x+3与x轴正半轴交于A点,与y轴正半轴交于点C,点F在抛物线上,且在第二象限,CE⊥OF于点E,连AC、AE.若AE=AC,求直线OF的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠BAD=90°,射线AC平分∠BAE.
如图,∠BAD=90°,射线AC平分∠BAE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4}$=±2 | B. | ±$\sqrt{16}$=4 | C. | $\root{3}{-8}$=-2 | D. | -$\sqrt{(-3)^{2}}$=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com