
| A. | $\sqrt{4}$=±2 | B. | ±$\sqrt{16}$=4 | C. | $\root{3}{-8}$=-2 | D. | -$\sqrt{(-3)^{2}}$=3 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
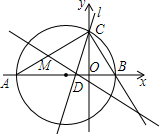 在平面直角坐标系中,△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆与y轴正半轴交于点C,A、B两点的横坐标xA、xB是关于x的方程x2+3x-4=0的两个根.
在平面直角坐标系中,△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆与y轴正半轴交于点C,A、B两点的横坐标xA、xB是关于x的方程x2+3x-4=0的两个根.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
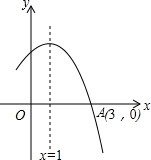 如图所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(3,0),二次函数图象对称轴为直线x=1,给出五个结论:①bc>0;②a+b+c<0;③当x<1时,y随x的增大而增大;④方程ax2+bx+c=0的根为x1=-1,x2=3;⑤4a-2b+c>0其中正确结论是( )
如图所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(3,0),二次函数图象对称轴为直线x=1,给出五个结论:①bc>0;②a+b+c<0;③当x<1时,y随x的增大而增大;④方程ax2+bx+c=0的根为x1=-1,x2=3;⑤4a-2b+c>0其中正确结论是( )| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 概念学习
概念学习查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始 数连续的正整数1,2,3,4…,当数到12时,对应的字母是B;当字母C第201次出现时,恰好数到的数是603.
如图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始 数连续的正整数1,2,3,4…,当数到12时,对应的字母是B;当字母C第201次出现时,恰好数到的数是603.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
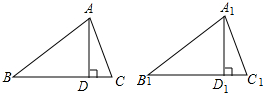 如图所示,AD、A1D1分别是锐角△ABC和△A1B1C1中边BC、B1C1的高,且AB=A1B1,AD=A1D1,若要使△ABC≌△A1B1C1,可补充的条件是∠C=∠C1(只需要填写一个你认为适当的条件即可)
如图所示,AD、A1D1分别是锐角△ABC和△A1B1C1中边BC、B1C1的高,且AB=A1B1,AD=A1D1,若要使△ABC≌△A1B1C1,可补充的条件是∠C=∠C1(只需要填写一个你认为适当的条件即可)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com