
【题目】如图,直线![]() 分别交x轴、y轴于A、B两点,直线BC与x轴交于点
分别交x轴、y轴于A、B两点,直线BC与x轴交于点![]() ,P是线段AB上的一个动点
,P是线段AB上的一个动点![]() 点P与A、B不重合
点P与A、B不重合![]() .
.

(1)求直线BC所对应的的函数表达式;
(2)设动点P的横坐标为t,![]() 的面积为S.
的面积为S.
①求出S与t的函数关系式,并写出自变量t的取值范围;
②在线段BC上存在点Q,使得四边形COPQ是平行四边形,求此时点Q的坐标.
【答案】(1)y=2x+4;(2)①S=-2t+8(0<t<4);②点Q的坐标为(![]() ,
,![]() ).
).
【解析】
(1)根据函数表达式求出点B坐标,结合点C坐标求出BC的表达式;
(2)①根据三角形面积求法可得S与t的表达式;
②过点P作PQ∥x轴,交BC于点Q,得出P和Q的坐标,利用平行四边形的性质建立方程求解即可.
解:(1)直线y=-x+4与x轴、y轴交点坐标分别为A(4,0)、B(0,4)两点.
设直线BC所对应的函数关系式为y=kx+4.
∵直线BC经过点C(-2,0),
∴-2k+4=0,解得:k=2,
∴直线BC所对应的函数关系式为y=2x+4.
(2)①由题意,设点P的坐标为(t,-t+4),
∴S=S△POA=![]() ×OA×yP=
×OA×yP=![]() ×4×(-t+4)=-2t+8.
×4×(-t+4)=-2t+8.
即S=-2t+8(0<t<4).
②过点P作PQ∥x轴,交BC于点Q.
∵点P的坐标为(t,-t+4),
∴点Q的坐标为(![]() ,-t+4).
,-t+4).
∵四边形COPQ是平行四边形,
∴PQ=OC,即![]() .
.
解得:t=![]() ,
,
∴点Q的坐标为(![]() ,
,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:我们把![]() 称为二阶行列式,规定它的运算法则为
称为二阶行列式,规定它的运算法则为![]() =ad﹣bc,例如:
=ad﹣bc,例如:![]() =2×5﹣3×4=﹣2.
=2×5﹣3×4=﹣2.
(1)填空:若![]() =0,则x= ,
=0,则x= ,![]() >0,则x的取值范围 ;
>0,则x的取值范围 ;
(2)若对于正整数m,n满足,1![]() <3,求m+n的值;
<3,求m+n的值;
(3)若对于两个非负数x,y,![]() =
=![]() =k﹣1,求实数k的取值范围.
=k﹣1,求实数k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
(1)写出A、B、C的坐标.
(2)以原点O为中心,将△ABC围绕原点O逆时针旋转180°得到△A1B1C1,画出△A1B1C1.
(3)求(2)中C到C1经过的路径以及OB扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
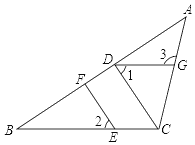
(1)试说明DG∥BC的理由;
(2)如果∠B=34°,且∠ACD=47°,求∠3的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】岳飞是我国古代宋朝的民族英雄,曾任通泰镇抚史、兼泰州知州.据说在泰州抗击金兵期间,有一次曾向将领们讲了如下一个布阵图,如图4是一座城池,在城池的四周设了八个哨所,一共由24个卫士把守,按直线算,每边都有11个人,后来由于军情发生变化,连续四次给哨所增添兵力,每次增加4人,但要求在增加人员后,仍然保持每边11个人把守.请问,兵力应如何调整?
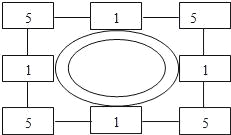
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下面的解题过程的横线上填空,并在括号内注明理由
.如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.

解:∵∠A=∠F(已知)
∴AC∥DF( )
∴∠D=∠ ( )
又∵∠C=∠D(已知)
∴∠1=∠C(等量代换)
∴BD∥CE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校研究性学习小组在研究有关二次函数及其图象性质的问题时,发现了两个重要结论.一是发现抛物线y=ax2+2x+3(a≠0),当实数a变化时,它的顶点都在某条直线上;二是发现当实数a变化时,若把抛物线y=ax2+2x+3的顶点的横坐标减少![]() ,纵坐标增加
,纵坐标增加![]() ,得到A点的坐标;若把顶点的横坐标增加
,得到A点的坐标;若把顶点的横坐标增加![]() ,纵坐标增加
,纵坐标增加![]() ,得到B点的坐标,则A、B两点一定仍在抛物线y=ax2+2x+3上.
,得到B点的坐标,则A、B两点一定仍在抛物线y=ax2+2x+3上.
(1)请你协助探求出当实数a变化时,抛物线y=ax2+2x+3的顶点所在直线的解析式;
(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它来吗?并说明理由;
(3)在他们第二个发现的启发下,运用“一般﹣一特殊﹣一般”的思想,你还能发现什么?你能用数学语言将你的猜想表述出来吗?你的猜想能成立吗?若能成立请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图点P是△ABC的边BC上的一动点,点E与点P关于直线AB成轴对称,连接EP交AB于点F,连接AP、EC相交于点O,连接AE.

(1)判断AE与AP的数量关系,并说明理由.
(2)在点P的运动过程中,当AE∥BC时,判断AP与BP的数量关系,并说明理由.
(3)若∠BAC=900,点P在运动过程中是否存在线段AP与线段EC互相平分的情况,若存在,请求出点P的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com