
����Ŀ����ͼ��Ҫ���һ���������εĻ�̳����̳�ϵ�![]() �ף��µ�
�ף��µ�![]() �ף����µ����
�ף����µ����![]() �ף��������е����ߣ����ߣ�����һ�������������µ�֮���������������������Ŀ�����ȣ������Ŀ�Ϊ
�ף��������е����ߣ����ߣ�����һ�������������µ�֮���������������������Ŀ�����ȣ������Ŀ�Ϊ![]() �ף�
�ף�
![]() �ú�
�ú�![]() ��ʽ�ӱ�ʾ�������������
��ʽ�ӱ�ʾ�������������
![]() �����������������������İ˷�֮һʱ�������Ŀ���
�����������������������İ˷�֮һʱ�������Ŀ���
![]() ������Ƶ�Ҫ�����Ŀ����ܳ���
������Ƶ�Ҫ�����Ŀ����ܳ���![]() �ף�����������ܷ��ã���Ԫ�������Ŀ��ȳ���������ϵ������ϵ����
�ף�����������ܷ��ã���Ԫ�������Ŀ��ȳ���������ϵ������ϵ����![]() ����̳���ಿ�ֵ��̻�����Ϊÿƽ����
����̳���ಿ�ֵ��̻�����Ϊÿƽ����![]() ��Ԫ����ô�����Ŀ���Ϊ������ʱ��������̳���ܷ������٣����ٷ����Ƕ�����Ԫ��
��Ԫ����ô�����Ŀ���Ϊ������ʱ��������̳���ܷ������٣����ٷ����Ƕ�����Ԫ��

���𰸡�![]() �����������Ϊ��
�������������![]() ��
��![]() ���Ŀ�Ϊ
���Ŀ�Ϊ![]() �ף�
�ף�![]() ���ٷ���Ϊ
���ٷ���Ϊ![]() ��Ԫ��
��Ԫ��
��������
��1������������״�����Σ����Ը������������ʽ������⣻
��2���ú�x�Ĵ���ʽ��ʾ�����������������Ȼ��������ε����������������ͨ�����������������İ˷�֮һ�з�����⣬����������Ҫע�����������غϲ��֣�
��3����ʾ������̳���ܷ��������Ŀ���֮��ĺ�����ϵʽ��ת���ɺ�������ֵ���������⼴�ɣ�
![]() �������������
�������������![]() ��
��
![]() �������������
�������������![]() ��
��
�������Ϊ![]() ��
��
�����⣺![]() ��
��
�����ã�![]() ��
��
![]() ��
��![]() �����������⣬��ȥ����
�����������⣬��ȥ����
�����Ŀ�Ϊ![]() �ף�
�ף�
![]() ��̳�ϵ�
��̳�ϵ�![]() �ף��µ�
�ף��µ�![]() �ף����µ����
�ף����µ����![]() �ף�
�ף�
�������������![]() ��
��
���������Ϊ![]() ��
��
�̻������Ϊ![]() ��
��
��̳�ܷ���![]() ���ܷ���+�̻��ܷ��ã�
���ܷ���+�̻��ܷ��ã�
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��![]() ʱ��
ʱ��![]() ��ֵ��С��
��ֵ��С��
�߸�����Ƶ�Ҫ�����Ŀ����ܳ���![]() �ף�
�ף�
�൱![]() ��ʱ���ܷ������٣�
��ʱ���ܷ������٣�
�����ٷ���Ϊ��![]() ��Ԫ��
��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵxOy�У���A������Ϊ��4��0�����Ե�AΪԲ�ģ�4Ϊ�뾶��Բ��x�ύ��O��B���㣬OCΪ�ң���AOC=60�㣬P��x���ϵ�һ���㣬����CP��
��1��ֱ��д��OC=___________��
��2����ͼ1����CP���A����ʱ����PO�ij���
��3����ͼ2������P��ֱ��OB��ʱ��CP���ӳ������A�ཻ�ڵ�Q���ʵ�POΪ��ֵʱ����OCQ�ǵ��������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ľߵ�����۸ֱʺͱʼDZ�������ÿ֧�ֱʶ���10Ԫ��ÿ���ʼDZ�����5Ԫ�������ľߵ��ڿ�չ������У���������Żݷ������£�
�꣺��һ֧�ֱ���һ���ʼDZ���
�ҵ꣺��ֱʻ�ʼDZ��������۵�80%����.
��С��Ҫ����ֱ�30֧���ʼDZ�![]() ��(
��(![]() ��30)��
��30)��
��1�����ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��С�����깺��������Ϊ Ԫ��
��С�����ҵ깺��������Ϊ Ԫ��
��2����![]() 40ʱ�����ܰ�С�����һ����ΪʡǮ�Ĺ�������д����Ĺ�������˵�����ɣ�
40ʱ�����ܰ�С�����һ����ΪʡǮ�Ĺ�������д����Ĺ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
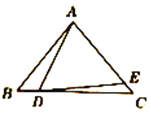
����Ŀ����ͼ��ʾ��D��E�ֱ��ǡ�ABC�ı�BC��AC�ϵĵ㣬��AB=AC��AD=AE.
��1������BAD=20�������EDC= ��.
��2������EDC=20�������BAD= ��.
��3�����BAD=������EDC=���������ɣ�1����2���еĽ���ҵ���������������Ĺ�ϵ��?��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E����DBC�ı�DB�ϣ���A����DBC�ڲ�����DAE=��BAC=90�㣬AD=AE��AB=AC���������н��ۣ�
��BD=CE���ڡ�ABD+��ECB=45�㣻��BD��CE����BE2=2��AD2+AB2����CD2��������ȷ���ǣ�������

A. �٢ڢۢ� B. �ڢ� C. �٢ڢ� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90����AC=BC=AD��

��1������A��ƽ���߽�CD��E��
��2����B��CD�Ĵ��ߣ�����ΪF��
��3����д��ͼ������ȫ�������Σ��������κ���ĸ������ѡ������һ�Լ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ĺ���
���![]() ��
��![]() ������
������
��1����������ͼ����![]() ��ǡ��һ�����㣬��
��ǡ��һ�����㣬��![]() ��ֵ��
��ֵ��
��2����������ͼ���������ߣ��Ҷ���ʼ����![]() ���Ϸ�����
���Ϸ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ABCD�У�O�ǶԽ���AC���е㣬����O��AC�Ĵ������AD��BC�ֱ���E��F.�ı���AFCE����������˵������.
ABCD�У�O�ǶԽ���AC���е㣬����O��AC�Ĵ������AD��BC�ֱ���E��F.�ı���AFCE����������˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У��Ե�AΪԲ�ģ�AB��Ϊ�뾶������AD�ڵ�F���ٷֱ��Ե�B��FΪԲ�ģ�����![]() ��Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
��Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��

��1���ı���ABEF��_______����ѡ����Ρ����Ρ������Ρ���ȷ������ֱ����д�����
��2��AE��BF�ཻ�ڵ�O�����ı���ABEF���ܳ�Ϊ40��BF=10����AE�ij�Ϊ________����ABC=________������ֱ����д�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com