
【题目】已知关于![]() 的函数
的函数![]() (
(![]() 为常数)
为常数)
(1)若函数的图象与![]() 轴恰有一个交点,求
轴恰有一个交点,求![]() 的值;
的值;
(2)若函数的图象是抛物线,且顶点始终在![]() 轴上方,求
轴上方,求![]() 的取值范围.
的取值范围.
【答案】(1)当a=0或a=![]() 时函数图象与
时函数图象与![]() 轴恰有一个交点;(2)当a>
轴恰有一个交点;(2)当a>![]() 或a<0时,抛物线顶点始终在
或a<0时,抛物线顶点始终在![]() 轴上方.
轴上方.
【解析】试题分析:(1)需考虑a为0和不为0的情况,当a=0时图象为一直线;当a≠0时图象是一抛物线,由判别式△=b2-4ac判断;
(2)根据抛物线顶点的纵坐标公式得到纵坐标,根据题意列出不等式组则可解.
试题解析:(1)当a=0时,函数为y=x+1,它的图象显然与![]() 轴只有一个交点(-1,0),
轴只有一个交点(-1,0),
当a≠0时,依题意得方程ax2+x+1=0有两等实数根,∴△=1-4a,∴a=![]() ,
,
∴当a=0或a=![]() 时函数图象与
时函数图象与![]() 轴恰有一个交点;
轴恰有一个交点;
(2)根据题意得![]() ,则
,则 ![]() 或
或![]() ,解得a>
,解得a>![]() 或a<0.
或a<0.
∴当a>![]() 或a<0时,抛物线顶点始终在
或a<0时,抛物线顶点始终在![]() 轴上方.
轴上方.


科目:初中数学 来源: 题型:
【题目】取一副三角板按如图所示拼接,固定三角板ADC,将三角板ABC绕点A顺时针方向旋转,旋转角度为α(0°<α≤45°),得到△ABC′.
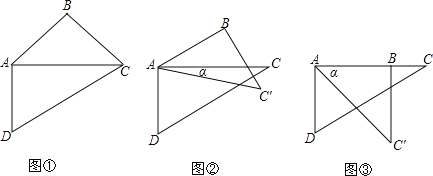
①当α为多少度时,AB∥DC?
②当旋转到图③所示位置时,α为多少度?
③连接BD,当0°<α≤45°时,探求∠DBC′+∠CAC′+∠BDC值的大小变化情况,并给出你的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC, ∠C=90°,CD 是AB边上的高, AC=4cm,BC=3cm,以点C为圆心作⊙C,使A、B、D三点至少有一个在圆内,且至少有一个在圆外,则⊙C半径r范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要设计一个等腰梯形的花坛,花坛上底![]() 米,下底
米,下底![]() 米,上下底相距
米,上下底相距![]() 米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为
米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为![]() 米.
米.
![]() 用含
用含![]() 的式子表示横向甬道的面积;
的式子表示横向甬道的面积;
![]() 当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
![]() 根据设计的要求,甬道的宽不能超过
根据设计的要求,甬道的宽不能超过![]() 米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是
米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是![]() ,花坛其余部分的绿化费用为每平方米
,花坛其余部分的绿化费用为每平方米![]() 万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(不比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
(2)图①中,a等于多少?D等级所占的圆心角为多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
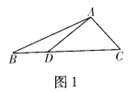
【题目】(1)探索发现
如图1,在△ABC中,点D在边BC上,△ABD与△ADC面积分别记为S1和S2,试判断![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(2)阅读分析
小东遇到这样一个问题:如图2,在Rt△ABC中,AB=AC,∠BAC=90°,射线AM交BC于点D,点E,F在AM上,且∠CEM=∠BFM=90°,试判断BF,CE,EF三条线段之间的数量关系.
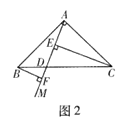
小东利用一对全等三角形,经过推理使问题得以解决.
填空:①图2中的一对全等三角形为_________;
②BF,CE,EF三条线段之间的数量关系为__________________.
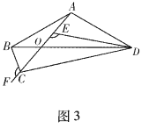
(3)类比探究
如图3,在四边形ABCD中,AB=AD,AC与BD交于点O,点E、F在射线AC上,且∠BCF=∠DEF=∠BAD.
①判断BC,DE,CE三条线段之间的数量关系,并说明理由;
②若OD=3OB,△AED的面积为2,直接写出四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多好佳水果店在批发市场购买某种水果销售,第一次用1500元购进若干千克,并以每千克9元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1694元所购买的水果比第一次多20千克,以每千克10元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价45%售完剩余的水果.
(1)第一次水果的进价是每千克多少元?
(2)该水果店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系XOY中,一次函数![]() 的图象是直线l1,l1与x轴、y轴分别相交于A、B两点.直线l2过点C(a,0)且与直线l1垂直,其中a>0.点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位.
的图象是直线l1,l1与x轴、y轴分别相交于A、B两点.直线l2过点C(a,0)且与直线l1垂直,其中a>0.点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位.
(1)写出A点的坐标和AB的长;
(2)当点P、Q运动了多少秒时,以点Q为圆心,PQ为半径的⊙Q与直线l2、y轴都相切,求此时a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
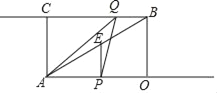
【题目】如图,已知矩形AOBC中.OB=3个单位,BC=4个单位,动点P从点A出发,沿射线AO以每秒4个单位长度的速度运动.同时动点Q从点B出发,沿射线BC以每秒2个单位的速度运动,设运动时间为t秒.
(1)用t表示线段PO的长度;
(2)当t为何值时,四边形APQC是矩形;
(3)设△APO与△AOB的重叠部分的面积为s平方单位,求s关于t的函数关系式;
(4)过点P作PE⊥AO交直线AB于点E,在动点P、Q运动的过程中,点H是平面内一点,当以B、Q、E、H为顶点的四边形是菱形时,请直接写出运动时间t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com