
【题目】(1)探索发现
如图1,在△ABC中,点D在边BC上,△ABD与△ADC面积分别记为S1和S2,试判断![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
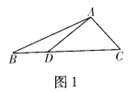
(2)阅读分析
小东遇到这样一个问题:如图2,在Rt△ABC中,AB=AC,∠BAC=90°,射线AM交BC于点D,点E,F在AM上,且∠CEM=∠BFM=90°,试判断BF,CE,EF三条线段之间的数量关系.
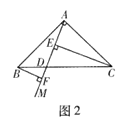
小东利用一对全等三角形,经过推理使问题得以解决.
填空:①图2中的一对全等三角形为_________;
②BF,CE,EF三条线段之间的数量关系为__________________.
(3)类比探究
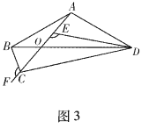
如图3,在四边形ABCD中,AB=AD,AC与BD交于点O,点E、F在射线AC上,且∠BCF=∠DEF=∠BAD.
①判断BC,DE,CE三条线段之间的数量关系,并说明理由;
②若OD=3OB,△AED的面积为2,直接写出四边形ABCD的面积.
【答案】(1)![]() =
=![]() ;(2)①△AEC≌△BFA,②EC=EF+BF; (3)①DE=BC+CE, ②8
;(2)①△AEC≌△BFA,②EC=EF+BF; (3)①DE=BC+CE, ②8
【解析】
(1)过点A作AE![]() BC,然后根据三角形面积公式求得两个三角形的面积,即可得出答案;(2)依据AAS可证明△AEC≌△BFA,由全等三角形的性质可得,AE=BF,EC=AF,由AF=EF+AE,通过等量代换即可得出答案;
BC,然后根据三角形面积公式求得两个三角形的面积,即可得出答案;(2)依据AAS可证明△AEC≌△BFA,由全等三角形的性质可得,AE=BF,EC=AF,由AF=EF+AE,通过等量代换即可得出答案;
(3)①依据AAS可证明△ABC≌△DAE,通过等量代换即可得出答案,②因为△AED的面积为2,根据全等三角形的性质可得S△ABC=2,然后根据(1)中的结论可求S△ADC=3S△ABC=6,即可得到答案.
解:(1)![]() =
=![]() ,
,
理由:如图,过点A作AE![]() BC,
BC,

∵S1=S△ABD=BD![]() AE,S2= S△ADC=DC
AE,S2= S△ADC=DC![]() AE,
AE,
∴![]() =
=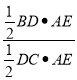 =
=![]() ;
;
(2)①△AEC≌△BFA,
理由:∵∠CEM=∠BFM=90°,
∴∠BFA=∠AEC=90°,
∴∠ABF+∠BFA=90°,
又∵∠BFA+∠FAC=90°,
∴∠ABF=∠EAC,
∵∠BFA=∠AEC=90°,
∠ABF=∠EAC,AB=AC,
∴△AEC≌△BFA.
②EC=EF+BF,
理由:∵△AEC≌△BFA,
∴AE=BF,EC=AF,
又∵AF=EF+AE,
∴EC=EF+BF.
(3)①DE=BC+CE,
理由:∵∠BCF=∠DEF,
∴∠AED=∠BCA,
∵∠ADE+∠EAD=∠DEF,
∠ABF+∠FAD=∠BAD,
∠DEF=∠BAD,
∴∠BAF=∠ADE,
∵∠AED=∠BCA,
∠BAC=∠ADE,AB=AD,
∴△ABC≌△DAE,
∴BC=AE,DE=AC,
又∵AC=AE+EC,
∴DE=BC+CE.
②∵△ABC≌△DAE, S△AED=2,
∴S△ABC=2,
∵OD=3OB,
∴![]() ,
,![]() ,
,
∴S△ADC=3S△ABC=6,
∴S四边形ABCD= S△ADC+ S△ABC=8.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,对角线AC,BD交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且cos∠BOE=![]() .求证:CB是⊙O的切线.
.求证:CB是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
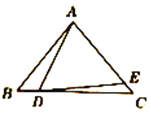
【题目】如图所示,D、E分别是△ABC的边BC、AC上的点,且AB=AC,AD=AE.
(1)若∠BAD=20°,则∠EDC= °.
(2)若∠EDC=20°,则∠BAD= °.
(3)设∠BAD=α,∠EDC=β,你能由(1)(2)中的结果找到α、β间所满足的关系吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=AD.

(1)作∠A的平分线交CD于E;
(2)过B作CD的垂线,垂足为F;
(3)请写出图中两对全等三角形(不添加任何字母),并选择其中一对加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且![]() .连接PB,试探究PA,PB,PC满足的等量关系.
.连接PB,试探究PA,PB,PC满足的等量关系.

图1 图2
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到![]() ,连接
,连接![]() ,如图1所示.
,如图1所示.
由![]() ≌
≌![]() 可以证得
可以证得![]() 是等边三角形,再由
是等边三角形,再由![]() 可得∠APC的大小为 度,进而得到
可得∠APC的大小为 度,进而得到![]() 是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
(2)如图2,当α=120°时,请参考(1)中的方法,探究PA,PB,PC满足的等量关系,并给出证明;
(3)PA,PB,PC满足的等量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300![]() 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),

(1)求围栏的长和宽;
(2)能否围成面积为400 ![]() 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
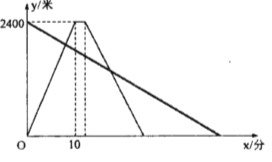
【题目】小明租用共享单车从家出发,匀速骑行到相距2400米的邮局办事.小明出发的同时,他的奶奶以每分钟60米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速的![]() 返回,如图是两人离家的距离
返回,如图是两人离家的距离![]() (米)与小明出发的时间
(米)与小明出发的时间![]() (分)之间的函数图象,根据图象信息解答下列问题:
(分)之间的函数图象,根据图象信息解答下列问题:
(1)小明去时的速度为______米/分;
(2)出发后______分钟两人第一次相遇;
(3)直接写出奶奶离家的距离与时间的关系式(不必写出自变量的取值范围);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com