
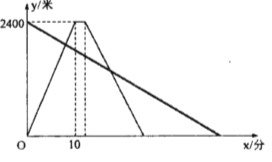
ЁОЬтФПЁПаЁУїзтгУЙВЯэЕЅГЕДгМвГіЗЂЃЌдШЫйЦяааЕНЯрОр2400УзЕФгЪОжАьЪТ.аЁУїГіЗЂЕФЭЌЪБЃЌЫћЕФФЬФЬвдУПЗжжг60УзЕФЫйЖШДггЪОжбиЭЌвЛЬѕЕРТЗВНааЛиМвЃЌаЁУїдкгЪОжЭЃСєСЫ2ЗжжгКѓбидТЗАДдЫйЕФ![]() ЗЕЛиЃЌШчЭМЪЧСНШЫРыМвЕФОрРы
ЗЕЛиЃЌШчЭМЪЧСНШЫРыМвЕФОрРы![]() (Уз)гыаЁУїГіЗЂЕФЪБМф
(Уз)гыаЁУїГіЗЂЕФЪБМф![]() (Зж)жЎМфЕФКЏЪ§ЭМЯѓЃЌИљОнЭМЯѓаХЯЂНтД№ЯТСаЮЪЬт:
(Зж)жЎМфЕФКЏЪ§ЭМЯѓЃЌИљОнЭМЯѓаХЯЂНтД№ЯТСаЮЪЬт:
(1)аЁУїШЅЪБЕФЫйЖШЮЊ______Уз/ЗжЃЛ
(2)ГіЗЂКѓ______ЗжжгСНШЫЕквЛДЮЯргіЃЛ
(3)жБНгаДГіФЬФЬРыМвЕФОрРыгыЪБМфЕФЙиЯЕЪН(ВЛБиаДГіздБфСПЕФШЁжЕЗЖЮЇ)ЃЛ
ЁОД№АИЁП(1)240 (2)![]() (3)
(3)![]()
ЁОНтЮіЁП
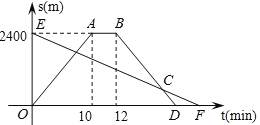
(1)гЩЬтПЩжЊЃЌаЁУїДгМвЕНгЪОж2400УзгУСЫ10ЗжжгЃЌПЩвдЧѓГіЫйЖШ.
(2)ЪзЯШгЩаЁУїФЬФЬУПЗжжг60УзДггЪОжЭЌвЛЬѕЕРТЗВНааЛиМвЃЌЧѓЕУаЁУїЕФФЬФЬгУЕФЪБМфЃЌМДПЩЕУЕуDЕФзјБъЃЌШЛКѓгЩEЁЂFзјБъПЩЧѓГівЛДЮКЏЪ§БэДяЪНгУEЁЂDзјБъПЩЧѓГіБэДяЪНЃЌШЛКѓСЊСЂЧѓГіНЛЕуКсзјБъМДПЩЃЛ
(3)(2)жаЫљЧѓжБЯпEFБэДяЪНЃЌМДЮЊЫљЧѓЃЎ
НтЃК(1)![]() Уз/ЗжЃЌ
Уз/ЗжЃЌ
ЙЪД№АИЮЊЃК240;
(2)гЩЬтвтжЊЃКаЁУїЗЕЛиЕФЫйЖШЮЊ![]() Уз/ЗжЃЌ
Уз/ЗжЃЌ
гЩЭМжЊЃК
ЫљвдЗЕЛиЕНМвЕФЪБМфЮЊ![]() Зж,
Зж,
![]() ,
,
ЩшЙ§BЁЂDЕФжБЯпБэДяЪНЮЊ![]() ,
,
АбBЁЂDЕуЕФзјБъДњШыМДЃК
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
![]() Й§BЁЂDЕФжБЯпБэДяЪНЮЊ
Й§BЁЂDЕФжБЯпБэДяЪНЮЊ![]() ЃЌ
ЃЌ
ФЬФЬЛиМвЕФЪБМфЮЊЃК![]() ЗжЃЌ
ЗжЃЌ
ЩшЙ§EЁЂFЕФжБЯпБэДяЪНЮЊ![]() ,
,
АбEЁЂFЕуЕФзјБъДњШыМДЃК
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
![]() Й§EЁЂFЕФжБЯпБэДяЪНЮЊ
Й§EЁЂFЕФжБЯпБэДяЪНЮЊ![]()
ЧѓГіНЛЕуCЕФКсзјБъЃК
![]() ,
,
НтЕУЃК![]() ЃЌ
ЃЌ
МДдк![]() ЗжЪБЯргі.
ЗжЪБЯргі.
(3)гЩ(2)ПЩЕУЃКЙиЯЕЪНЮЊ![]() .
.


 аЁбЇНЬВФЭъШЋНтЖСЯЕСаД№АИ
аЁбЇНЬВФЭъШЋНтЖСЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(1)ЬНЫїЗЂЯж
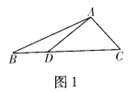
ШчЭМ1ЃЌдкЁїABCжаЃЌЕуDдкБпBCЩЯЃЌЁїABDгыЁїADCУцЛ§ЗжБ№МЧЮЊS1КЭS2ЃЌЪдХаЖЯ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩ.
ЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩ.
(2)дФЖСЗжЮі
аЁЖЋгіЕНетбљвЛИіЮЪЬтЃКШчЭМ2ЃЌдкRtЁїABCжаЃЌAB=ACЃЌЁЯBAC=90ЁуЃЌЩфЯпAMНЛBCгкЕуDЃЌЕуEЃЌFдкAMЩЯЃЌЧвЁЯCEM=ЁЯBFM=90ЁуЃЌЪдХаЖЯBFЃЌCEЃЌEFШ§ЬѕЯпЖЮжЎМфЕФЪ§СПЙиЯЕ.
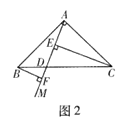
аЁЖЋРћгУвЛЖдШЋЕШШ§НЧаЮЃЌОЙ§ЭЦРэЪЙЮЪЬтЕУвдНтОі.
ЬюПеЃКЂйЭМ2жаЕФвЛЖдШЋЕШШ§НЧаЮЮЊ_________ЃЛ
ЂкBFЃЌCEЃЌEFШ§ЬѕЯпЖЮжЎМфЕФЪ§СПЙиЯЕЮЊ__________________.
(3)РрБШЬНОП
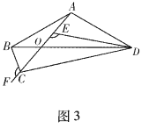
ШчЭМ3ЃЌдкЫФБпаЮABCDжаЃЌAB=ADЃЌACгыBDНЛгкЕуOЃЌЕуEЁЂFдкЩфЯпACЩЯЃЌЧвЁЯBCF=ЁЯDEF=ЁЯBAD.
ЂйХаЖЯBCЃЌDEЃЌCEШ§ЬѕЯпЖЮжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЂкШєOD=3OBЃЌЁїAEDЕФУцЛ§ЮЊ2ЃЌжБНгаДГіЫФБпаЮABCDЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
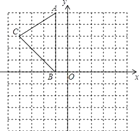
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌAЃЈЉ1ЃЌ5ЃЉЃЌBЃЈЉ1ЃЌ0ЃЉЃЌCЃЈЉ4ЃЌ3ЃЉЃЎ
ЃЈ1ЃЉдкЭМжазїГіЁїABCЙигкyжсЕФЖдГЦЭМаЮЁїA1B1C1ЃЛ
ЃЈ2ЃЉдкyжсЩЯевГівЛЕуPЃЌЪЙЕУPA+PBЕФжЕзюаЁЃЌжБНгаДГіЕуPЕФзјБъЃЛ
ЃЈ3ЃЉдкЦНУцжБНЧзјБъЯЕжаЃЌевГівЛЕуA2ЃЌЪЙЁїA2BCгыЁїABCЙигкжБЯпBCЖдГЦЃЌжБНгаДГіЕуA2ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКМзЁЂввСНГЕЗжБ№ДгЯрОр300kmЕФA,BСНЕиЭЌЪБГіЗЂЯрЯђЖјааЃЌМзЕНBЕиКѓСЂМДЗЕЛиЃЌЯТЭМЪЧЫќУЧРыИїздГіЗЂЕиЕФОрРыyгыааЪЛЪБМфxжЎМфЕФКЏЪ§ЭМЯѓ.
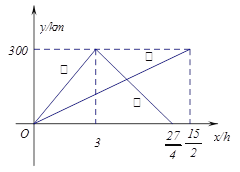
ЃЈ1ЃЉЧѓМзГЕРыГіЗЂЕиЕФОрРыyгыааЪЛЪБМфxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂБъУїздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєвбжЊввГЕааЪЛЕФЫйЖШЪЧ40ЧЇУз/аЁЪБЃЌЧѓГіЗЂКѓЖрГЄЪБМфЃЌСНГЕРыИїздГіЗЂЕиЕФОрРыЯрЕШЃЛ
ЃЈ3ЃЉЫќУЧдкааЪЛЙ§ГЬжагаМИДЮЯргі.ВЂЧѓГіУПДЮЯргіЕФЪБМф.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
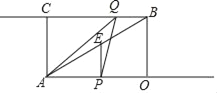
ЁОЬтФПЁПШчЭМЃЌвбжЊОиаЮAOBCжаЃЎOB=3ИіЕЅЮЛЃЌBC=4ИіЕЅЮЛЃЌЖЏЕуPДгЕуAГіЗЂЃЌбиЩфЯпAOвдУПУы4ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЎЭЌЪБЖЏЕуQДгЕуBГіЗЂЃЌбиЩфЯпBCвдУПУы2ИіЕЅЮЛЕФЫйЖШдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉгУtБэЪОЯпЖЮPOЕФГЄЖШЃЛ
ЃЈ2ЃЉЕБtЮЊКЮжЕЪБЃЌЫФБпаЮAPQCЪЧОиаЮЃЛ
ЃЈ3ЃЉЩшЁїAPOгыЁїAOBЕФжиЕўВПЗжЕФУцЛ§ЮЊsЦНЗНЕЅЮЛЃЌЧѓsЙигкtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ4ЃЉЙ§ЕуPзїPEЁЭAOНЛжБЯпABгкЕуEЃЌдкЖЏЕуPЁЂQдЫЖЏЕФЙ§ГЬжаЃЌЕуHЪЧЦНУцФквЛЕуЃЌЕБвдBЁЂQЁЂEЁЂHЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЪБЃЌЧыжБНгаДГідЫЖЏЪБМфtЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбОиаЮжНЦЌABCDбиЖдНЧЯпелЕўЃЌЩшжиЕўВПЗжЮЊЁїEBDЃЌФЧУДЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ

A. ЁїEBDЪЧЕШбќШ§НЧаЮЃЌEB=ED B. елЕўКѓЁЯABEКЭЁЯCЁфBDвЛЖЈЯрЕШ
C. елЕўКѓЕУЕНЕФЭМаЮЪЧжсЖдГЦЭМаЮ D. ЁїEBAКЭЁїEDCЁфвЛЖЈЪЧШЋЕШШ§НЧаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊУРЛЏаЃдАЃЌМЦЛЎАВХХМзввСНИіЪЉЙЄЖгЙВЭЌНјааТЬЛЏЃЎвбжЊМзЖгУПЬьЭъГЩТЬЛЏУцЛ§ЪЧввЖгУПЬьЭъГЩТЬЛЏУцЛ§ЕФ2БЖЃЛЧвМзввСНЖгЗжБ№ЭъГЩ400m2ЕФТЬЛЏУцЛ§ЪБЃЌМзЖгБШввЖгЩйгУ4ЬьЃЎ
ЃЈ1ЃЉЧѓМзЁЂввСНЖгУПЬьФмЭъГЩЕФТЬЛЏУцЛ§ЗжБ№ЪЧЖрЩйm2ЃП
ЃЈ2ЃЉбЇаЃУПЬьашИЖИјМзЖгЕФТЬЛЏЗбгУЮЊ0.4ЭђдЊЃЌввЖгЮЊ0.25ЭђдЊЃЎвбжЊбЇаЃМЦЛЎТЬЛЏУцЛ§1800m2ЃЌвЊЪЙетДЮЕФТЬЛЏзмЗбгУВЛГЌЙ§8ЭђдЊЃЌжСЩйгІАВХХМзЖгЙЄзїЖрЩйЬьЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
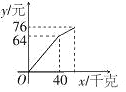
ЁОЬтФПЁПаЁУїдкЪюЦкЩчЛсЪЕМљЛюЖЏжаЃЌвдУПЧЇПЫ0.8дЊЕФМлИёДгХњЗЂЪаГЁЙКНјШєИЩЧЇПЫЮїЙЯЕНЪаГЁЩЯШЅЯњЪлЃЌдкЯњЪлСЫ40ЧЇПЫЮїЙЯжЎКѓЃЌгрЯТЕФУПЧЇПЫНЕМл0.4дЊЃЌШЋВПЪлЭъ.ЯњЪлН№ЖюгыЪлГіЮїЙЯЕФЧЇПЫЪ§жЎМфЕФЙиЯЕШчЭМЫљЪО.ЧыФуИљОнЭМЯѓЬсЙЉЕФаХЯЂЭъГЩвдЯТЮЪЬтЃК
(1)ЧѓНЕМлЧАЯњЪлН№Жюy(дЊ)гыЪлГіЮїЙЯx(ЧЇПЫ)жЎМфЕФКЏЪ§ЙиЯЕЪН.
(2)аЁУїДгХњЗЂЪаГЁЙВЙКНјЖрЩйЧЇПЫЮїЙЯ?
(3)аЁУїетДЮТєЙЯзЌСЫЖрЩйЧЎ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвдOЮЊдВаФЕФСНИіЭЌаФдВжаЃЌаЁдВЕФЯвABЕФбгГЄЯпНЛДѓдВгкЕуCЃЌШєAB=3ЃЌBC=1ЃЌдђгыдВЛЗЕФУцЛ§зюНгНќЕФећЪ§ЪЧЃЈ ЃЉ

A. 9 B. 10 C. 15 D. 13
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com