
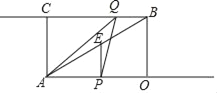
����Ŀ����ͼ����֪����AOBC�У�OB=3����λ��BC=4����λ������P�ӵ�A������������AO��ÿ��4����λ���ȵ��ٶ��˶���ͬʱ����Q�ӵ�B������������BC��ÿ��2����λ���ٶ��˶������˶�ʱ��Ϊt�룮
��1����t��ʾ�߶�PO�ij��ȣ�
��2����tΪ��ֵʱ���ı���APQC�Ǿ��Σ�
��3������APO����AOB���ص����ֵ����Ϊsƽ����λ����s����t�ĺ�����ϵʽ��
��4������P��PE��AO��ֱ��AB�ڵ�E���ڶ���P��Q�˶��Ĺ����У���H��ƽ����һ�㣬����B��Q��E��HΪ������ı���������ʱ����ֱ��д���˶�ʱ��t��ֵ��
���𰸡���1����0��t��1ʱ��PO=4��4t����t��1ʱ��PO=4t��4����2����t= ![]() ʱ���ı���APQC�Ǿ�������3��s��4t;(4)
ʱ���ı���APQC�Ǿ�������3��s��4t;(4) ![]()
��������
(1)��������������п��ǣ�������P���߶�AO�ϣ���P������AO�ϣ�(2)����������ó���AP=4t��CQ=4��2t�����ݾ��ε����ʵó�AP=CQ���Ӷ��ó��𰸣�(3)���١���0��t��1ʱ���ص������ǡ�ADP������DM��OA��M����BC��N���������������Ƶó��𰸣���t��1ʱ���ص��������ı���ADKO����DM��OA��M����BC��N��PQ��OB��K��������������߶εij��ȣ�Ȼ����������(4)����������������м��㣬����BEΪ���εĶԽ��ߣ���BE=BQ����BQ�����εĶԽ��ߣ���BE=BQʱ���ֱ��ĸ�ͼ�Σ��Ӷ��ó��𰸣�
��1����0��t��1ʱ��PO=4��4t����t��1ʱ��PO=4t��4��
��2��AP=4t��CQ=4��2t����APQC�Ǿ���ʱ����AP=CQ�� ��4t=4��2t����t=![]()
��t= ![]() ʱ���ı���APQC�Ǿ��Σ�
ʱ���ı���APQC�Ǿ��Σ�
��3������ͼ1�У���0��t��1ʱ���ص������ǡ�ADP����DM��OA��M����BC��N��

��BQ=2t��AP=4t��BQ��AP����![]() =
=![]() =
=![]() =
=![]() �� ��AC=OB=3����DM=
�� ��AC=OB=3����DM=![]() ��3=2��
��3=2��
��s=![]() ��
��
����ͼ2�У���t��1ʱ���ص��������ı���ADKO����DM��OA��M����BC��N��PQ��OB��K��
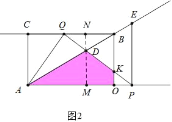
��OP��BQ����![]() =
=![]() ����
����![]() =
=![]() ����OK=
����OK=![]() ��
��
��![]() ��
��
��4������ͼ3�У���BEΪ���εĶԽ���ʱ��
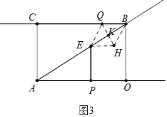
���ı���EQBH�����Σ���EK=BK=![]() ��5��5t������
��5��5t������![]() =cos��ABC=
=cos��ABC=![]() ����
����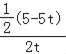 =
=![]() ��
��
��t=![]() ��
��
����ͼ4 �У���BE=BQʱ��
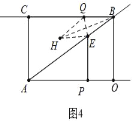
����5��5t=2t��t=![]() ��
��
����ͼ5�У���BQ�����εĶԽ���ʱ��
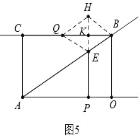
��cos��ABC=![]() ���ɵã�
���ɵã�![]() =
=![]() �����t=
�����t=![]() ��
��
����ͼ6�У���BE=BQʱ��5t��5=2t�����t=![]() ��
��
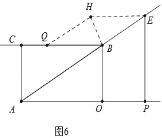
������������������ʱt��ֵΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ĺ���
���![]() ��
��![]() ������
������
��1����������ͼ����![]() ��ǡ��һ�����㣬��
��ǡ��һ�����㣬��![]() ��ֵ��
��ֵ��
��2����������ͼ���������ߣ��Ҷ���ʼ����![]() ���Ϸ�����
���Ϸ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����9�֣�ij��������ÿ��50Ԫ�ļ۸�800��T������һ�����Ե���80Ԫ���ۣ��۳���200�����ڶ�����������۲��䣬Ԥ���Կ��۳�200����������Ϊ�����������������������ۣ������г����飬����ÿ����1Ԫ���ɶ��۳�10��������͵���Ӧ���ڹ����ļ۸ڶ����½����������̽���ʣ���T��һ����������ۣ�����ǵ���Ϊ40Ԫ����ڶ����µ��۽���![]() Ԫ��
Ԫ��
��1������������軯��

��2�����������ϣ��ͨ����������T������9000Ԫ����ô�ڶ����µĵ���Ӧ�Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У��Ե�AΪԲ�ģ�AB��Ϊ�뾶������AD�ڵ�F���ٷֱ��Ե�B��FΪԲ�ģ�����![]() ��Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
��Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��

��1���ı���ABEF��_______����ѡ����Ρ����Ρ������Ρ���ȷ������ֱ����д�����
��2��AE��BF�ཻ�ڵ�O�����ı���ABEF���ܳ�Ϊ40��BF=10����AE�ij�Ϊ________����ABC=________������ֱ����д�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
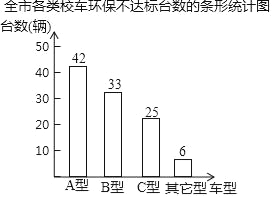
����Ŀ�������ж�ȫ�и��ࣨA�͡�B�͡�C�ͣ������ͣ�У����848�����л�������ղ飬�ղ�������Ƴ���������ͳ��ͼ��
��1����ȫ�и���������У����������
��2����ȫ��848��У���л��������У���İٷֱȣ�
��3���涨���������У���������ά�ޣ�����Ϊ��A��500Ԫ/����B��1000Ԫ/����C��600Ԫ/����������300Ԫ/������ȫ����Ҫ����ά�Ļ��������У��ά�ѵ��ܺͣ�
��4����ÿ��У������40��ѧ������ôһ����ά��ȫ�������У������Ӱ��ȫ��80000��ѧ����У����ѧ�İٷֱ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
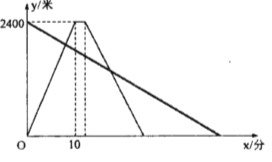
����Ŀ��С�����ù��������Ӽҳ������������е����2400���ʾְ���.С��������ͬʱ������������ÿ����60���ٶȴ��ʾ���ͬһ����·���лؼң�С�����ʾ�ͣ����2���Ӻ���ԭ·��ԭ�ٵ�![]() ���أ���ͼ��������ҵľ���
���أ���ͼ��������ҵľ���![]() (��)��С��������ʱ��
(��)��С��������ʱ��![]() (��)֮��ĺ���ͼ����ͼ����Ϣ�����������:
(��)֮��ĺ���ͼ����ͼ����Ϣ�����������:
(1)С��ȥʱ���ٶ�Ϊ______��/�֣�
(2)������______�������˵�һ��������
(3)ֱ��д��������ҵľ�����ʱ��Ĺ�ϵʽ(����д���Ա�����ȡֵ��Χ)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���μ䣬��Ƥ��С��������ʦ�ĵ���ֱ�����ǰ���ںڰ��ϻ����˵�ƽ��ֱ������ϵ��(��ͼ)����ֱ֪�Ƕ���H������Ϊ(0��1)����һ������G������Ϊ(4��4)�����K������Ϊ___________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������4���������У�����AB=AC���������ε�һ�������һ��ֱ���ܹ�����������ηֳ�����С���������ε��ǣ�������

A. �٢�B. �٢ڢ�C. �٢ۢ�D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB>BC,AB=AC,DE��AB�Ĵ�ֱƽ���ߣ�����ΪD�㣬��AC�ڵ�E.
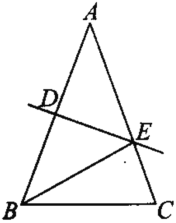
��1������ABE=40�������EBC�Ķ�����
��2������ABC���ܳ�Ϊ41cm��һ��Ϊ15cm������BCE���ܳ�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com