
【题目】已知Rt△ABC, ∠C=90°,CD 是AB边上的高, AC=4cm,BC=3cm,以点C为圆心作⊙C,使A、B、D三点至少有一个在圆内,且至少有一个在圆外,则⊙C半径r范围是_____.

科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠A=40°,求∠DBC的度数.
(2)若△BCD的周长为16cm,△ABC的周长为26cm,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实践与操作:
根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).

(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF.
猜想并证明:
判断四边形AECF的形状并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个文具店均出售钢笔和笔记本,其中每支钢笔定价10元,每本笔记本定价5元.两个文具店在开展促销活动中,各自提出优惠方案如下:
甲店:买一支钢笔送一本笔记本;
乙店:买钢笔或笔记本都按定价的80%付款.
现小明要购买钢笔30支,笔记本![]() 本(
本(![]() >30).
>30).
(1)试用含![]() 的代数式表示:
的代数式表示:
①小明到甲店购买所付款为 元;
②小明到乙店购买所付款为 元;
(2)当![]() 40时,你能帮小明设计一种最为省钱的购买方案吗?试写出你的购买方案,并说明理由.
40时,你能帮小明设计一种最为省钱的购买方案吗?试写出你的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,AD=4,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,且垂足H在边AD上,连接AF.
(1)求证:FH=ED;
(2)设AE=x,是否存在某个x的值,使得△AEF的面积为3?若存在,求出x的值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
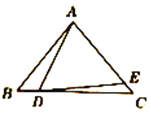
【题目】如图所示,D、E分别是△ABC的边BC、AC上的点,且AB=AC,AD=AE.
(1)若∠BAD=20°,则∠EDC= °.
(2)若∠EDC=20°,则∠BAD= °.
(3)设∠BAD=α,∠EDC=β,你能由(1)(2)中的结果找到α、β间所满足的关系吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是( )

A. ①②③④ B. ②④ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com