
【题目】(本题满分8分)如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实践与操作:
根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).

(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF.
猜想并证明:
判断四边形AECF的形状并加以证明.
【答案】(1)见解析;(2)见解析
【解析】
试题(1)根据题意画出图形即可;
(2)首先根据等腰三角形的性质与三角形内角与外角的性质证明∠ACB=∠FAC,进而可得AF∥BC;然后再根据线段的垂直平分线的性质可知:OA=OC, ∠AOF=∠COE=90°,AE=EC,FA=FC,由OA=OC, ∠AOF=∠COE=90°,∠CAM=∠ACB可证明AOF≌△COE,即可得到AF=EC.因此可由AF∥BC,AF=EC,得证四边形AECF是平行四边形.最后可由AC⊥EF得证结论:菱形.
试题解析:(1)

(2)猜想:四边形AECF是菱形
证明:∵AB=AC ,AM平分∠CAD
∴∠B=∠ACB,∠CAD=2∠CAM
∵∠CAD是△ABC的外角
∴∠CAD=∠B+∠ACB
∴∠CAD=2∠ACB
∴∠CAM=∠ACB
∴AF∥CE
∵EF垂直平分AC
∴OA=OC, ∠AOF=∠COE=![]()
∴AOF≌△COE
∴AF=CE
在四边形AECF中,AF∥CE,AF=CE
∴四边形AECF是平行四边形
又∵EF⊥AC
∴四边形AECF是菱形


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() 、
、![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
![]() 求该函数的表达式;
求该函数的表达式;
![]() 点
点![]() 为该函数在第一象限内的图象上一点,过点
为该函数在第一象限内的图象上一点,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() .
.
①求线段![]() 的最大值;
的最大值;
②若以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】基本图形:在Rt△![]() 中,
中,![]() ,
,![]() 为
为![]() 边上一点(不与点
边上一点(不与点![]() ,
,![]() 重合),将线段
重合),将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() .
.
探索:(1)连接![]() ,如图①,试探索线段
,如图①,试探索线段![]() 之间满足的等量关系,并证明结论;
之间满足的等量关系,并证明结论;
(2)连接![]() ,如图②,试探索线段
,如图②,试探索线段![]() 之间满足的等量关系,并证明结论;
之间满足的等量关系,并证明结论;

联想:(3)如图③,在四边形![]() 中,
中,![]() .若
.若![]() ,
,![]() ,则
,则![]() 的长为 .
的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】取一副三角板按如图所示拼接,固定三角板ADC,将三角板ABC绕点A顺时针方向旋转,旋转角度为α(0°<α≤45°),得到△ABC′.
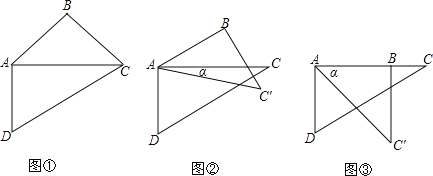
①当α为多少度时,AB∥DC?
②当旋转到图③所示位置时,α为多少度?
③连接BD,当0°<α≤45°时,探求∠DBC′+∠CAC′+∠BDC值的大小变化情况,并给出你的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )

A. 4 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(4,5)、B(1,0)、C(4,0).
(1)画出△ABC关于y轴的对称图形△A1B1C1,并写出A1点的坐标;
(2)在y轴上求作一点P,使△PAB的周长最小,并求出点P的坐标及△PAB的周长最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王欲开一家品牌服装店,向朋友借了![]() 元用于店面装修.已知该品牌服装进价为每件
元用于店面装修.已知该品牌服装进价为每件![]() 元,预测日销售量
元,预测日销售量![]() (件)与销售价
(件)与销售价![]() (元/件)之间的关系如下:
(元/件)之间的关系如下:![]() .
.
该店应支付员工的工资为每人每天![]() 元,每天还应支付其它费用为
元,每天还应支付其它费用为![]() 元(不包括借款).
元(不包括借款).
![]() 若该店某天的销售价为
若该店某天的销售价为![]() 元/件时,当天正好收支平衡(其中支出
元/件时,当天正好收支平衡(其中支出![]() 服装成本+员工工资+应支付其它费用),求该店员工的人数;
服装成本+员工工资+应支付其它费用),求该店员工的人数;
![]() 若该店只有
若该店只有![]() 名员工,设该服装店每天的毛利润为
名员工,设该服装店每天的毛利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式;(毛利润
之间的函数关系式;(毛利润![]() 销售收入-服装成本-员工工资-应支付其它费用)
销售收入-服装成本-员工工资-应支付其它费用)
![]() 在
在![]() 的条件下,若每天毛利润全部用于还款,而所借款每天应按万分之二的利率支付利息,则该店最少需要多少天(取整数)才能还清借款?此时每件服装的价格应定为多少元?
的条件下,若每天毛利润全部用于还款,而所借款每天应按万分之二的利率支付利息,则该店最少需要多少天(取整数)才能还清借款?此时每件服装的价格应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC, ∠C=90°,CD 是AB边上的高, AC=4cm,BC=3cm,以点C为圆心作⊙C,使A、B、D三点至少有一个在圆内,且至少有一个在圆外,则⊙C半径r范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多好佳水果店在批发市场购买某种水果销售,第一次用1500元购进若干千克,并以每千克9元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1694元所购买的水果比第一次多20千克,以每千克10元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价45%售完剩余的水果.
(1)第一次水果的进价是每千克多少元?
(2)该水果店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com