练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    若正方形的对角线长为
    		2
    ，则它的面积为（　　）
    A、1
    B、
    		2
    C、2
    D、2
    		2
    考点：正方形的性质
    专题：
    分析：根据正方形的性质，对角线平分、相等、垂直且平分每一组对角求解即可．
    解答：解：∵四边形ABCD是正方形，
    ∴AO=BO=
    1
    2
    AC=
    		2
    2
    ，
    ∵∠AOB=90°，
    由勾股定理得，AB=1，
    S正方形ABCD=1×1=1．
    故选A．
    点评：本题考查了正方形的性质，对角线平分、相等、垂直且平分每一组对角以及勾股定定理的运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知y-1与x成反比例，且当x=1时，y=4，则当y=3时，x=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知D、E在△ABC的边上，DE∥BC，∠B=60°，∠AED=45°，则∠A的度数为（　　）
    A、65°B、75°
    C、85°D、95°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知如图，按要求画图
    ①画直线AB；
    ②连接AC、CD，并延长CD至E点，使CE=2CD；
    ③画射线CB；
    ④在图上找一P点，使点P到A、B、C、D四点的距离和最小值（请保留做题痕迹）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    25
    16
    =
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）计算：
    		18
    -(π-1)0-2cos45°+(
    1
    4
    )-1
    （2）解下列不等式组：
    x+5≥2x+2
    2+
    2
    3
    x＞
    4
    3
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，点A在双曲线y=
    k
    x
    上，点C在x轴正半轴上，过点A、C分别作x轴、y轴的平行线，交点为B，D为BC的中点，连接AD，OD．若OC=BC，∠OAD=∠AOC，S△AOD=
    5
    4
    ，则k的值为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

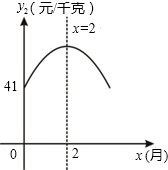
    已知：某大型水果种植中心对去年某种时令水果的销售情况统计如下：上半年的销售单价y1（元/千克）与月份x（月）（1≤x≤6，且x为整数）的关系．如下表所示：
    x（月） 1 2 3 4 5 6
    y1（元/千克） 36 18 12 9 7.2 6
    下半年的销售单价y2（元/千克）与月份x（月）（7≤x≤12，且x为整数）的函数关系为y2=ax2+4x+c，其图象如图所示．同时，去年上半年的销售量为z1（万千克）与月份x（月）（1≤x≤6，且x为整数）的函数关系式为z1=x2-x；去年下半年的销量一直稳定在每月10万千克．
    （1）请观察题目中的表格及图象，用所学过的一次函数、二次函数或反比例函数的相关知识，直接写出y1与x的函数关系式，及y2与x的函数关系式．
    （2）试求出去年哪个月的销售额最大？最大销售额是多少万元？
    （3）进入今年1月份后，由于全市物价上涨，该种植中心决定将去年取得最大销售额时的单价提高了3a%，销量却在去年12月份的基础上下降了0.5a%，进入2月份，该种植中心再次调整策略，决定将去年取得最大销售额时的单价扩大3.2倍，销量与今年1月份持平．这样，1月份、2月份两个月的销售总额一共可达到860万元，试求出a的最大整数值．（参考数据：
    		21
    ≈4.68，
    		22
    ≈4.75，
    		23
    ≈4.82    ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在水上治安指挥塔A西侧两条航线l1、l2上有两艘巡逻艇B与C（C所在航线靠近A），直线l1、l2间的距离CD=
    		3
    km，点B在点A的南偏西30°方向上，且AB=6km，A在C的北偏东60°方向上．求：
    （1）巡逻艇C与塔A之间的距离AC．（结果保留根号）
    （2）已知巡逻艇C的速度每小时比巡逻艇B快5km，当两艘巡逻艇同时到达指挥塔A的正南方向时，求巡逻艇B的速度．

    查看答案和解析>>

    同步练习册答案