
分析 (1)仿照题中的规律将原式变形,计算即可得到结果;
(2)归纳总结得到一般性规律,写出即可;
(3)根据题意列出方程,利用得出的规律变形,计算即可求出n的值.
解答 解:(1)原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{6}$=1-$\frac{1}{6}$=$\frac{5}{6}$;
(2)根据题意得:原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$;
(3)根据题意得:$\frac{1}{3}$(1-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{7}$+…+$\frac{1}{3n-2}$-$\frac{1}{3n+1}$)=$\frac{15}{46}$,即$\frac{1}{3}$(1-$\frac{1}{3n+1}$)=$\frac{15}{46}$,
解得:n=15.
故答案为:(1)$\frac{5}{6}$;(2)$\frac{n}{n+1}$
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
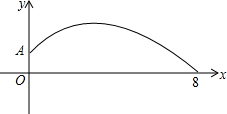 某学校在一次投掷铅球时,刚出手时铅球离地面$\frac{5}{3}$m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图所示:
某学校在一次投掷铅球时,刚出手时铅球离地面$\frac{5}{3}$m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
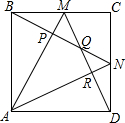 如图,M、N是单位正方形ABCD边BC、CD的中点,连接AM、DM、AN、BN,则这些线段所围成的四边形APQR的面积是$\frac{4}{15}$.
如图,M、N是单位正方形ABCD边BC、CD的中点,连接AM、DM、AN、BN,则这些线段所围成的四边形APQR的面积是$\frac{4}{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{50x+40(12-x)≥520}\\{15x+25(12-x)≥240}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{50x+40(12-x)>520}\\{15x+25(12-x)>240}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{50x+40(12-x)≤520}\\{15x+25(12-x)≤240}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{50x+40(12-x)<520}\\{15x+25(12-x)<240}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com