
【题目】(定义学习)
定义:如果四边形有一组对角为直角,那么我们称这样的四边形为“对直四边形”
(判断尝试)
在①梯形;②矩形:③菱形中,是“对直四边形”的是哪一个. (填序号)
(操作探究)
在菱形ABCD中,![]() 于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,
于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,

(实践应用)
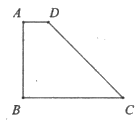
某加工厂有一批四边形板材,形状如图所示,若AB=3米,AD=1米,![]()
![]()
.现根据客户要求,需将每张四边形板材进一步分割成两个等腰三角形板材和一个“对直四边形"板材,且这两个等腰三角形的腰长相等,要求材料充分利用无剩余.求分割后得到的等腰三角形的腰长,
【答案】【判断尝试】②;【操作探究】EF的长为2,EF的长为![]() ;【实践应用】方案1:两个等腰三角形的腰长都为
;【实践应用】方案1:两个等腰三角形的腰长都为![]() 米.理由见解析,方案2:两个等腰三角形的腰长都为2米.理由见解析,方案3:两个等腰三角形的腰长都为
米.理由见解析,方案2:两个等腰三角形的腰长都为2米.理由见解析,方案3:两个等腰三角形的腰长都为![]() 米,理由见解析.方案4:两个等腰三角形的腰长都为
米,理由见解析.方案4:两个等腰三角形的腰长都为![]() 米,理由见解析.
米,理由见解析.
【解析】
[判断尝试]根据“对直四边形”定义和①梯形;②矩形:③菱形的性质逐一分析即可解答.
[操作探究]由菱形性质和30°直角三角形性质即可求得EF的长.
[实践应用]先作出“对直四边形”,容易得到另两个等腰三角形,再利用等腰三角形性质和勾股定理即可求出腰长.
解: [判断尝试]
①梯形不可能一组对角为直角;③菱形中只有正方形的一组对角为直角,②矩形四个角都是直角,故矩形有一组对角为直角,为“对直四边形”,
故答案为② ,
[操作探究]
F在边AD上时,如图:

∴四边形AECF是矩形,
∴AE=CE,
又∵![]() ,
,
∴BE=1,AE=![]() ,CE=AF=1,
,CE=AF=1,
∴在Rt△AEF中,EF=![]() =2
=2
EF的长为2.
F在边CD上时,AF⊥CD,
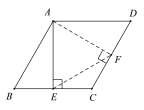
∵四边形ABCD是菱形,
∴AB=AD=2,∠B=∠D=60°,
又∵AE⊥BC,
∴∠BAE=∠BAF=30°,
∴AE=AF=![]() ,
,
∵∠BAD=120°,
∴∠EAF=60°,
∴△AEF为等边三角形,
∴EF=AF=AE=![]()
即:EF的长为![]() ;
;
故答案为2,![]() .
.
[实践应用]
方案1:如图①,作![]() ,则四边形ABCD分为等腰
,则四边形ABCD分为等腰![]() 、等腰
、等腰![]() 、“对直四边形”ABED,其中两个等腰三角形的腰长都为
、“对直四边形”ABED,其中两个等腰三角形的腰长都为![]() 米.
米.

理由:∵![]() ,∴
,∴
∴![]() 3米,
3米,
∵![]() ,
,
∴△DEC为等腰直角三角形,
∴DE=EC=3米,
∴DC=![]() 米,
米,
∵![]() ,
,
∴![]() =
=![]() DC=
DC=![]() 米.
米.
方案2:如图②,作![]() ,则四边形ABCD分为等腰△FEB、等腰△FEC、“对直四边形”ABED,其中两个等腰三角形的腰长都为2米.
,则四边形ABCD分为等腰△FEB、等腰△FEC、“对直四边形”ABED,其中两个等腰三角形的腰长都为2米.
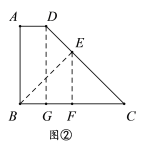
理由:作![]() ,由(1)可知
,由(1)可知![]() 3米,BG=AD=1米,
3米,BG=AD=1米,
∴BC=1+3=4米,
∵![]() ,
,
∴△BEC为等腰直角三角形,
∵![]() ,
,
∴![]()
![]() BC=2米.
BC=2米.
方案3:如图③,作CD、BC的垂直平分线交于点E,连接ED、EB,则四边形ABCD分为等腰△CED、等腰△CEB、“对直四边形”ABED,其中两个等腰三角形的腰长都为![]() 米.
米.

理由:连接CE,并延长交AB于点F,
∵CD、BC的垂直平分线交于点E,∴![]() ,∴
,∴![]() ,
,
∴![]()
![]() .
.
连接DB,
DB=![]() =
=![]() ,
,
∵ED=EB,
∴△BED为等腰直角三角形,
∴ED=![]() 米,
米,
∴![]()
![]() 米.
米.
方案4:如图④,作![]() ,交AB于点E,
,交AB于点E,![]() ,
,
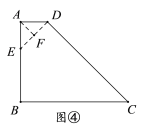
则四边形ABCD分为等腰△AFE、等腰△AFD、“对直四边形”BEDC,其中两个等腰三角形的腰长都为![]() 米.
米.
理由:作![]() ,交AB于点E,可证∠ADE
,交AB于点E,可证∠ADE![]() 45°,
45°,
∵![]() ,
,
∴△ADE为等腰直角三角形,
∴DE =![]() 米,
米,
作![]() ,
,
∴![]()
![]() DE=
DE=![]() 米.
米.


科目:初中数学 来源: 题型:
【题目】我国古代数学家刘徽发展了“重差术”,用于测量不可到达的物体的高度,比如,通过下列步骤可测量山的高度PQ(如图):
(1)测量者在水平线上的A处竖立一根竹竿,沿射线QA方向走到M处,测得山顶P、竹竿顶端B及M在一条直线上;
(2)将该竹竿竖立在射线QA上的C处,沿原方向继续走到N处,测得山顶P、竹竿顶端D及N在一条直线上;
(3)设竹竿与AM、CN的长分别为![]() 、a1、a2,可得公式:PQ=
、a1、a2,可得公式:PQ=![]() +
+![]() .则上述公式中,d表示的是( )
.则上述公式中,d表示的是( )
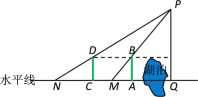
A. QA的长 B. AC的长 C. MN的长 D. QC的长
查看答案和解析>>
科目:初中数学 来源: 题型:
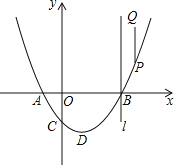
【题目】如图,已知抛物线![]() :
:![]() ,
,![]() 交x轴于A,
交x轴于A,![]() 点A在点B左边
点A在点B左边![]() ,交y轴于C,其顶点为D,P是
,交y轴于C,其顶点为D,P是![]() 上一个动点,过P沿y轴正方向作线段
上一个动点,过P沿y轴正方向作线段![]() 轴,使
轴,使![]() ,当P点在
,当P点在![]() 上运动时,Q随之运动形成的图形记为
上运动时,Q随之运动形成的图形记为![]() .
.
![]() 若
若![]() ,求点P运动到D点时点Q的坐标,并直接写出图形
,求点P运动到D点时点Q的坐标,并直接写出图形![]() 的函数解析式;
的函数解析式;
![]() 过B作直线
过B作直线![]() 轴,若直线l和y轴及
轴,若直线l和y轴及![]() ,
,![]() 所围成的图形面积为12,求t的值.
所围成的图形面积为12,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午![]() ,下午
,下午![]() ,每月
,每月![]() 天;
天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于![]() 件.
件.
生产产品件数与所用时间之间的关系见下表:
生产甲产品数(件) | 生产乙产品数(件) | 所用时间 (分) |
|
|
|
|
|
|
信息三:按件计酬:每生产一件甲产品可得![]() 元,每生产一件乙产品可得
元,每生产一件乙产品可得![]() 元.
元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟;
(2)小王该月最多能得多少元,此时生产甲、乙两种产品分别多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,在平面内,如果一个图形绕着一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转的这个角称为这个图形的一个旋转角.例如,正方形绕着它的对角线的交点旋转![]() 后能与自身重合所以正方形是旋转对称图形,它有一个旋转角为
后能与自身重合所以正方形是旋转对称图形,它有一个旋转角为![]() .
.
![]() 判断下列说法是否正确(在相应横线里填上“对”或“错”)
判断下列说法是否正确(在相应横线里填上“对”或“错”)
①正五边形是旋转对称图形,它有一个旋转角为![]() .________
.________
②长方形是旋转对称图形,它有一个旋转角为![]() .________
.________
![]() 填空:下列图形中时旋转对称图形,且有一个旋转角为
填空:下列图形中时旋转对称图形,且有一个旋转角为![]() 的是________.(写出所有正确结论的序号)
的是________.(写出所有正确结论的序号)
①正三角形②正方形③正六边形④正八边形
![]() 写出两个多边形,它们都是旋转对称图形,都有一个旋转角为
写出两个多边形,它们都是旋转对称图形,都有一个旋转角为![]() ,其中一个是轴对称图形,但不是中心对称图形;另一个既是轴对称图形,又是中心对称图形.
,其中一个是轴对称图形,但不是中心对称图形;另一个既是轴对称图形,又是中心对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )

A. ∠D=∠C B. BD=AC C. ∠CAD=∠DBC D. AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,∠BAC=θ.边 AB 的垂直平分线交边 BC 于点 D,边 AC的垂直平分线交边BC于点 E,连结 AD,AE,则∠DAE 的度数为_____.(用含θ 的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
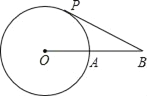
【题目】如图,⊙O的半径为6cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以π cm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为______时,BP与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们对垃圾分类知识的知晓程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识.某校环保社团的同学们设计了“垃圾分类知识及投放情况”的问卷,并在本校随机抽取了若干名同学进行了问卷测试,根据测试成绩分布情况,他们将全部成绩分成A,B,C,D四组,并绘制了如下不完整的统计图表:
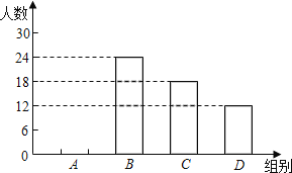
组别 | 分数段 | 频数 | 频率 |
A | 60≤x<70 | a | b |
B | 70≤x<80 | 24 | 0.4 |
C | 80≤x<90 | 18 | c |
D | 90≤x<100 | 12 | 0.2 |
请根据上述统计图表,解答下列问题:
(1)共抽取了多少名学生进行问卷测试?
(2)补全频数分布直方图;
(3)如果测试成绩不低于80分者为“优秀”,请你估计全校2000名学生中,“优秀”等次的学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com